题目内容
定义在R上的函数f(x)对任意两个不相等实数a,b,总有
>0成立,则必有( )
| f(a)-f(b) |
| a-b |
| A、f(x)在R上是增函数 |
| B、f(x)在R上是减函数 |
| C、函数f(x)是先增加后减少 |
| D、函数f(x)是先减少后增加 |
考点:函数单调性的判断与证明
专题:常规题型,函数的性质及应用
分析:由单调性的定义说明单调性即可.
解答:
解:∵定义在R上的函数f(x)对任意两个不相等实数a,b,总有
>0成立,
即对任意两个不相等实数a,b,
若a<b,总有f(a)<f(b)成立,
f(x)在R上是增函数.
故选A.
| f(a)-f(b) |
| a-b |
即对任意两个不相等实数a,b,
若a<b,总有f(a)<f(b)成立,
f(x)在R上是增函数.
故选A.
点评:本题考查了函数单调性的变形应用,属于基础题.

练习册系列答案
相关题目
从分别写有ABCDE的5张卡片中任取两张,两字母恰好相连的概率( )
| A、0.2 | B、0.4 |
| C、0.3 | D、0.7 |
计箅cos42°cos18°-cos48°sin18°的结果等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=
的定义域为( )
log
|
| A、(-∞,1] | ||
| B、[1,+∞) | ||
C、(
| ||
D、(
|
设a,b∈R,且i(a+i)=b-i,则a-b=( )
| A、2 | B、1 | C、0 | D、-2 |
二项式(2x+
)7的展开式中
的系数是( )
| 1 |
| x |
| 1 |
| x3 |
| A、42 | B、168 | C、84 | D、21 |
某流程图如图所示,现输入如下四个函数,则可以输出的函数是( )
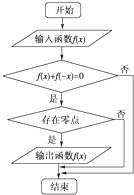

| A、f(x)=sinx | ||
| B、f(x)=cosx | ||
C、f(x)=
| ||
| D、f(x)=x2 |
将函数f(x)=sinx+cosx的图象向左平移φ(φ>0)个单位长度,所得图象关于原点对称,则φ的最小值为( )
A、-
| ||
B、
| ||
C、
| ||
D、
|