题目内容
17.甲、乙两人进行乒乓球比赛,约定每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或打满8局时停止.设甲在每局中获胜的概率为p(p>$\frac{1}{2}$),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为$\frac{5}{8}$.(Ⅰ)求p的值;
(Ⅱ)设ξ表示比赛停止时比赛的局数,求随机变量ξ的分布列和数学期望Eξ.
分析 (Ⅰ)由题意可知,当甲连胜2局或乙连胜2局时,第二局比赛结束时比赛停止,再由互斥事件的概率及相互独立事件的概率列式求p的值;
(Ⅱ)求出ξ的所有可能取值,得到ξ取不同值时的概率,得到分布列,代入期望公式求期望.
解答 解:(Ⅰ)当甲连胜2局或乙连胜2局时,第二局比赛结束时比赛停止,
故${p}^{2}+(1-p)^{2}=\frac{5}{8}$,解得p=$\frac{1}{4}$或p=$\frac{3}{4}$.
又p$>\frac{1}{2}$,∴p=$\frac{3}{4}$;
(Ⅱ)依题意知,ξ的所有可能取值为2,4,6,8.
p(ξ=2)=$\frac{5}{8}$;
p(ξ=4)=$(1-\frac{5}{8})×\frac{5}{8}=\frac{15}{64}$;
p(ξ=6)=$(1-\frac{5}{8})^{2}×\frac{5}{8}=\frac{45}{512}$;
p(ξ=8)=$(1-\frac{5}{8})^{3}=\frac{27}{512}$.
∴随机变量ξ的分布列为:
| ξ | 2 | 4 | 6 | 8 |
| p | $\frac{5}{8}$ | $\frac{15}{64}$ | $\frac{45}{512}$ | $\frac{27}{512}$ |
点评 本题考查离散型随机变量的期望与方差,训练了独立事件概率的求法,是中档题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
7.如图是某几何体的三视图,则该几何体的表面积为( )


| A. | 80+16$\sqrt{2}$+16$\sqrt{3}$ | B. | 80+12$\sqrt{2}$+16$\sqrt{3}$ | C. | 80+16$\sqrt{2}$+12$\sqrt{3}$ | D. | 80+12$\sqrt{2}$+12$\sqrt{3}$ |
12.对标有不同编号的形状大小完全一样的5件正品和3件次品进行检测,现不放回地依次取出2件,则在第一次取出正品的条件下,第二次也取出正品的概率是( )
| A. | $\frac{1}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{5}{14}$ | D. | $\frac{4}{7}$ |
6.如图所示,AB=AC=1,DC=2BD,DE=EA,cos∠BAC=$\frac{1}{3}$,则BE=( )
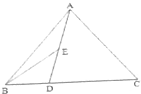

| A. | $\frac{59}{108}$ | B. | $\frac{43}{108}$ | C. | $\frac{\sqrt{177}}{18}$ | D. | $\frac{\sqrt{129}}{18}$ |
 如图,在三棱锥A-BCD中,AB⊥平面BCD,AC=AD=2,BC=BD=1,点E是线段AD的中点.
如图,在三棱锥A-BCD中,AB⊥平面BCD,AC=AD=2,BC=BD=1,点E是线段AD的中点.