题目内容
10.已知数列{an},Sn是其前n项的和且满足3an=2Sn+n(n∈N*),则Sn=$\frac{{3}^{n+1}-3-2n}{4}$.分析 3an=2Sn+n(n∈N*),n=1时,3a1=2a1+1,解得a1.n≥2时,可得:3an-3an-1=2an+1,化为an=3an-1+1,变形为:an$+\frac{1}{2}$=3(an-1+$\frac{1}{2}$),利用等比数列的通项公式可得an,进而得出Sn.
解答 解:∵3an=2Sn+n(n∈N*),
∴n=1时,3a1=2a1+1,解得a1=1.
n≥2时,3an-1=2Sn-1+(n-1),可得:3an-3an-1=2an+1,
化为an=3an-1+1,变形为:an$+\frac{1}{2}$=3(an-1+$\frac{1}{2}$),
∴数列$\{{a}_{n}+\frac{1}{2}\}$是等比数列,首项为$\frac{3}{2}$,公比为3.
∴an+$\frac{1}{2}$=$\frac{3}{2}$×3n-1,即an=$\frac{{3}^{n}}{2}$-$\frac{1}{2}$.
∴$3×\frac{1}{2}({3}^{n}-1)$=2Sn+n,解得Sn=$\frac{{3}^{n+1}-3-2n}{4}$.
故答案为:$\frac{{3}^{n+1}-3-2n}{4}$.
点评 本题考查了递推关系、等比数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知全集U=R,集合A={x|(x+2)(x-2)≤0},则集合∁RA=( )
| A. | (2,+∞) | B. | [2,+∞) | C. | (-∞,-2)∪(2,+∞) | D. | (-∞,-2]∪[2,+∞) |
1.“x>2”是“x2-2x>0”成立的( )
| A. | 既不充分也不必要条件 | B. | 充要条件 | ||
| C. | 必要而不充分条件 | D. | 充分而不必要条件 |
18.已知z是纯虚数,i为虚数单位,$\frac{z+2}{1-i}$在复平面内所对应的点在实轴上,那么z等于( )
| A. | 2i | B. | i | C. | -i | D. | -2i |
5.某校共有学生2000名,各年级男、女生人数如表中所示.已知在全校学生中随机抽取1名,抽到二年级女生的概率是0.18.现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为( )
| 一年级 | 二年级 | 三年级 | |
| 女生 | 363 | x | y |
| 男生 | 387 | 390 | z |
| A. | 12 | B. | 16 | C. | 18 | D. | 24 |
20.双曲线中,焦点为F1(-3,0),F2(3,0),实半轴a=2,则双曲线的方程是( )
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{5}$=1 | C. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{y}^{2}}{5}$-$\frac{{x}^{2}}{4}$=1 |
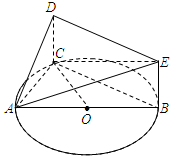 如图,AB是△ABC外接圆O的直径,四边形DCBE为矩形,且DC⊥平面ABC,AB=4,BE=1.
如图,AB是△ABC外接圆O的直径,四边形DCBE为矩形,且DC⊥平面ABC,AB=4,BE=1.