一个几何体的三视图如图所示.则该几何体的体积为( )A．$4\sqrt{3}+1$B．$4\sqrt{3}$C．$24+2\sqrt{3}+\sqrt{15}$D．$24+3\sqrt{3}+\sqrt{15}$ 题目和参考答案——青夏教育精英家教网—

题目内容

19．一个几何体的三视图如图所示（单位：m），则该几何体的体积为（　　）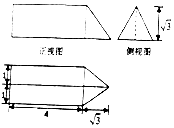

A．

$4\sqrt{3}+1$

B．

$4\sqrt{3}$

C．

$24+2\sqrt{3}+\sqrt{15}$

D．

$24+3\sqrt{3}+\sqrt{15}$

分析由题意，直观图是三棱柱与三棱锥的组合体，利用所给数据，求出体积．

解答解：由题意，直观图是三棱柱与三棱锥的组合体，
体积为$\frac{1}{2}×2×\sqrt{3}×4+\frac{1}{3}×\frac{1}{2}×2×\sqrt{3}×\sqrt{3}$=4$\sqrt{3}$+1．
故选A．

点评本题考查了棱锥的三视图和结构特征，属于基础题．

练习册系列答案

10．“2＜m＜6”是“方程$\frac{x^2}{m-2}+\frac{y^2}{6-m}$=1为双曲线的方程”的（　　）

	A．	充分不必要条件		B．	必要不充分条件
	C．	充要条件		D．	既不充分也不必要条件

7．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，φ∈（0，$\frac{π}{2}$））的图象在y轴上的截距为1，在相邻两个最值点$（{x_0}-\frac{3}{2}，2）$和（x₀，-2）上（x₀＞0），函数f（x）分别取最大值和最小值．
（1）求函数f（x）的解析式；
（2）若f（x）=$\frac{k+1}{2}$在区间$[0，\frac{3}{2}]$内有两个不同的零点，求k的取值范围；
（3）求函数f（x）在区间$[\frac{13}{4}，\frac{23}{4}]$上的对称轴方程．

14．已知回归方程$\stackrel{∧}{y}$=2x+1，而试验得到一组数据是（2，5.1），（3，6.9），（4，9.1），则残差平方和是（　　）

4．已知α为第三象限的角，且$sinα=-\frac{{\sqrt{5}}}{5}$，则tanα=$\frac{1}{2}$．

11．在数列{a_n}中，${a_1}=\frac{1}{2}，{a_n}_{+1}=1-\frac{1}{a_n}$，则a₅=（　　）

8．设（1+3i）（2a+i）的实部与虚部相等，其中a为实数，则a=（　　）

9．双曲线$\frac{y^2}{2}-{x^2}=1$的焦距是$2\sqrt{3}$；渐近线方程为$\sqrt{2}x±y=0$．

试题分类