题目内容
10.“2<m<6”是“方程$\frac{x^2}{m-2}+\frac{y^2}{6-m}$=1为双曲线的方程”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 方程$\frac{x^2}{m-2}+\frac{y^2}{6-m}$=1为双曲线的方程,则(m-2)(6-m)<0,m<2或m>6,即可得出结论.
解答 解:方程$\frac{x^2}{m-2}+\frac{y^2}{6-m}$=1为双曲线的方程,则(m-2)(6-m)<0,
∴m<2或m>6,
∴“2<m<6”是“方程$\frac{x^2}{m-2}+\frac{y^2}{6-m}$=1为双曲线的方程”的既不充分也不必要条件,
故选D.
点评 本题考查充要条件的判断,考查学生的计算能力,利用方程$\frac{x^2}{m-2}+\frac{y^2}{6-m}$=1为双曲线的方程,则(m-2)(6-m)<0,求出m的范围是关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
20.函数$y=\sqrt{3}sin2x+2{cos^2}x-1$的值域是( )
| A. | [-1,2] | B. | [-2,2] | C. | [-1,3] | D. | [0,4] |
1.若$0<{θ_1}<{θ_2}<\frac{π}{2}$,则必有( )
| A. | ${e^{cos{θ_1}}}-{e^{cos{θ_2}}}>lncos{θ_1}-lncos{θ_2}$ | |
| B. | ${e^{cos{θ_1}}}-{e^{cos{θ_2}}}<lncos{θ_1}-lncos{θ_2}$ | |
| C. | $cos{θ_2}{e^{cos{θ_1}}}>cos{θ_1}{e^{cos{θ_2}}}$ | |
| D. | $cos{θ_2}{e^{cos{θ_1}}}<cos{θ_1}{e^{cos{θ_2}}}$ |
18.已知a=0.5${\;}^{\frac{1}{3}}$,b=($\frac{3}{5}$)${\;}^{-\frac{1}{3}}$,c=log2.51.5,则a,b,c的大小关系( )
| A. | c<a<b | B. | b<a<c | C. | a<b<c | D. | c<b<a |
5.在△ABC中,如果有性质acosA=bcosB,这个三角形的形状是( )
| A. | 等边三角形 | B. | 等腰三角形 | ||
| C. | 等腰三角形或直角三角形 | D. | 等腰直角三角形 |
15.已知△ABC,|AB|=8,AC与BC边所在直线的斜率之积为定值m,
(1)求动点C的轨迹方程;
(2)当m=1时,过点E(0,1)的直线l与曲线C相交于P、Q两点,求P、Q两点的中点M的轨迹方程.
(1)求动点C的轨迹方程;
(2)当m=1时,过点E(0,1)的直线l与曲线C相交于P、Q两点,求P、Q两点的中点M的轨迹方程.
19.一个几何体的三视图如图所示(单位:m),则该几何体的体积为( )
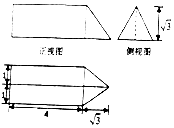

| A. | $4\sqrt{3}+1$ | B. | $4\sqrt{3}$ | C. | $24+2\sqrt{3}+\sqrt{15}$ | D. | $24+3\sqrt{3}+\sqrt{15}$ |
20. 从某小区随机抽取40个家庭,收集了这40个家庭去年的月均用水量(单位:吨)的数据,整理得到频数分布表和频率分布直方图.
从某小区随机抽取40个家庭,收集了这40个家庭去年的月均用水量(单位:吨)的数据,整理得到频数分布表和频率分布直方图.
(1)求频率分布直方图中a,b的值;
(2)从该小区随机选取一个家庭,试估计这个家庭去年的月均用水量不低于6吨的概率;
(3)在这40个家庭中,用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本,将该样本看成一个总体,从中任意选取2个家庭,求其中恰有一个家庭的月均用水量不低于8吨的概率.
 从某小区随机抽取40个家庭,收集了这40个家庭去年的月均用水量(单位:吨)的数据,整理得到频数分布表和频率分布直方图.
从某小区随机抽取40个家庭,收集了这40个家庭去年的月均用水量(单位:吨)的数据,整理得到频数分布表和频率分布直方图.| 分组 | 频数 |
| [2,4) | 2 |
| [4,6) | 10 |
| [6,8) | 16 |
| [8,10) | 8 |
| [10,12] | 4 |
| 合计 | 40 |
(2)从该小区随机选取一个家庭,试估计这个家庭去年的月均用水量不低于6吨的概率;
(3)在这40个家庭中,用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本,将该样本看成一个总体,从中任意选取2个家庭,求其中恰有一个家庭的月均用水量不低于8吨的概率.