已知全集U={-1.2.3.a}.集合M={-1.3}．若∁UM={2.5}.则实数a的值为5．题目和参考答案——青夏教育精英家教网——

题目内容

9．已知全集U={-1，2，3，a}，集合M={-1，3}．若∁_UM={2，5}，则实数a的值为5．

分析求出集合M的补集，根据对应关系求出a的值即可．

解答解：∵集合M={-1，3}，
∴∁_UM={2，5}={2，a}，
故a=5，
故答案为：5．

点评本题考查了集合的运算，考查补集的定义以及集合的性质，是一道基础题．

练习册系列答案

中考说明与训练系列答案

中考备考每天一点系列答案

征服英语名师课时计划系列答案

考前系列答案

口算心算快速算系列答案

跨越中考总复习方略系列答案

新语文阅读训练系列答案

秒杀口算题系列答案

口算题卡加应用题集训系列答案

中考1加1系列答案

相关题目

19．若sinα＜0，tanα＞0，则α的终边在（　　）

、第二象限

20．函数$y=\sqrt{3}sin2x+2{cos^2}x-1$的值域是（　　）

17．已知函数$f（x）=cos（\frac{π}{2}+x）+{sin^2}（\frac{π}{2}+x）$，x∈[-π，0]，则f（x）的最大值为（　　）

4．$f（x）=1o{g_{\frac{1}{2}}}（sinxcosx+{cos^2}x）$的单调递减区间为[kπ-$\frac{π}{4}$，kπ+$\frac{π}{8}$]（k∈Z）．

14．已知${（{x+1}）^2}{（{x+2}）^{2016}}={a_0}+{a_1}（{x+2}）+{a_2}{（{x+2}）^2}+…+{a_{2018}}{（{x+2}）^{2018}}$，则$\frac{a_1}{2}+\frac{a_2}{2^2}+\frac{a_3}{2^3}+…+\frac{{{a_{2018}}}}{{{2^{2018}}}}$的值是（$\frac{1}{2}$）²⁰¹⁸．

1．若$0＜{θ_1}＜{θ_2}＜\frac{π}{2}$，则必有（　　）

	A．	${e^{cos{θ_1}}}-{e^{cos{θ_2}}}＞lncos{θ_1}-lncos{θ_2}$
	B．	${e^{cos{θ_1}}}-{e^{cos{θ_2}}}＜lncos{θ_1}-lncos{θ_2}$
	C．	$cos{θ_2}{e^{cos{θ_1}}}＞cos{θ_1}{e^{cos{θ_2}}}$
	D．	$cos{θ_2}{e^{cos{θ_1}}}＜cos{θ_1}{e^{cos{θ_2}}}$

18．已知a=0.5${\;}^{\frac{1}{3}}$，b=（$\frac{3}{5}$）${\;}^{-\frac{1}{3}}$，c=log_2.51.5，则a，b，c的大小关系（　　）

19．一个几何体的三视图如图所示（单位：m），则该几何体的体积为（　　）

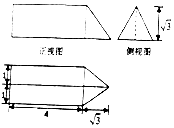
$24+2\sqrt{3}+\sqrt{15}$

$24+3\sqrt{3}+\sqrt{15}$