题目内容
9.双曲线$\frac{y^2}{2}-{x^2}=1$的焦距是$2\sqrt{3}$;渐近线方程为$\sqrt{2}x±y=0$.分析 根据题意,由双曲线的标准方程可得其焦点在y轴上,则a=$\sqrt{2}$,b=1,计算可得c的值,由焦距公式以及渐近线方程计算可得答案.
解答 解:根据题意,双曲线的方程为$\frac{y^2}{2}-{x^2}=1$,
其焦点在y轴上,则a=$\sqrt{2}$,b=1,
则其c=$\sqrt{2+1}$=$\sqrt{3}$,
故其焦距2c=2$\sqrt{3}$,
渐近线方程y=±$\sqrt{2}$x,即$\sqrt{2}x±y=0$;
故答案为:$2\sqrt{3}$;$\sqrt{2}x±y=0$.
点评 本题考查双曲线的标准方程,注意双曲线标准方程的形式以及有双曲线标准方程确定焦点位置的方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.一个几何体的三视图如图所示(单位:m),则该几何体的体积为( )
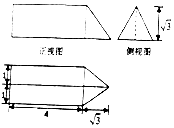

| A. | $4\sqrt{3}+1$ | B. | $4\sqrt{3}$ | C. | $24+2\sqrt{3}+\sqrt{15}$ | D. | $24+3\sqrt{3}+\sqrt{15}$ |
20. 从某小区随机抽取40个家庭,收集了这40个家庭去年的月均用水量(单位:吨)的数据,整理得到频数分布表和频率分布直方图.
从某小区随机抽取40个家庭,收集了这40个家庭去年的月均用水量(单位:吨)的数据,整理得到频数分布表和频率分布直方图.
(1)求频率分布直方图中a,b的值;
(2)从该小区随机选取一个家庭,试估计这个家庭去年的月均用水量不低于6吨的概率;
(3)在这40个家庭中,用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本,将该样本看成一个总体,从中任意选取2个家庭,求其中恰有一个家庭的月均用水量不低于8吨的概率.
 从某小区随机抽取40个家庭,收集了这40个家庭去年的月均用水量(单位:吨)的数据,整理得到频数分布表和频率分布直方图.
从某小区随机抽取40个家庭,收集了这40个家庭去年的月均用水量(单位:吨)的数据,整理得到频数分布表和频率分布直方图.| 分组 | 频数 |
| [2,4) | 2 |
| [4,6) | 10 |
| [6,8) | 16 |
| [8,10) | 8 |
| [10,12] | 4 |
| 合计 | 40 |
(2)从该小区随机选取一个家庭,试估计这个家庭去年的月均用水量不低于6吨的概率;
(3)在这40个家庭中,用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本,将该样本看成一个总体,从中任意选取2个家庭,求其中恰有一个家庭的月均用水量不低于8吨的概率.
11.若A${\;}_{m}^{5}$=2A${\;}_{m}^{3}$,则m的值为( )
| A. | 5 | B. | 3 | C. | 6 | D. | 7 |