题目内容
给出命题:
(1)在空间里,垂直于同一平面的两个平面平行;
(2)设l,m是不同的直线,α是一个平面,若l⊥α,l∥m,则m⊥α;
(3)已知α,β表示两个不同平面,m为平面α内的一条直线,则“α⊥β”是“m⊥β”的充要条件;
(4)m、n表示直线,α、β、γ表示平面,若α⊥β,α∩γ=m,β∩γ=n,则n⊥m;
(5)m表示直线,α、β表示平面,若m⊥α,m⊥β,则α∥β.
其中正确的命题是 (只填序号).
(1)在空间里,垂直于同一平面的两个平面平行;
(2)设l,m是不同的直线,α是一个平面,若l⊥α,l∥m,则m⊥α;
(3)已知α,β表示两个不同平面,m为平面α内的一条直线,则“α⊥β”是“m⊥β”的充要条件;
(4)m、n表示直线,α、β、γ表示平面,若α⊥β,α∩γ=m,β∩γ=n,则n⊥m;
(5)m表示直线,α、β表示平面,若m⊥α,m⊥β,则α∥β.
其中正确的命题是
考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:利用空间中线线、线面、面面间的位置关系求解.
解答:
解:(1)在空间里,垂直于同一平面的两个平面平行或相交,故(1)错误;
(2)设l,m是不同的直线,α是一个平面,
若l⊥α,l∥m,则由直线与平南垂直的判定定理得m⊥α,故(2)正确;
(3)已知α,β表示两个不同平面,m为平面α内的一条直线,
则“α⊥β”是“m⊥β”的不充分不必要条件,故(3)错误;
(4)m、n表示直线,α、β、γ表示平面,
若α⊥β,α∩γ=m,β∩γ=n,则n与m相交、平行或异面,故(4)错误;
(5)m表示直线,α、β表示平面,若m⊥α,m⊥β,
则由平面与平面平行的判定定理得α∥β,故(5)正确.
故答案为:(2)(5)
(2)设l,m是不同的直线,α是一个平面,
若l⊥α,l∥m,则由直线与平南垂直的判定定理得m⊥α,故(2)正确;
(3)已知α,β表示两个不同平面,m为平面α内的一条直线,
则“α⊥β”是“m⊥β”的不充分不必要条件,故(3)错误;
(4)m、n表示直线,α、β、γ表示平面,
若α⊥β,α∩γ=m,β∩γ=n,则n与m相交、平行或异面,故(4)错误;
(5)m表示直线,α、β表示平面,若m⊥α,m⊥β,
则由平面与平面平行的判定定理得α∥β,故(5)正确.
故答案为:(2)(5)
点评:本题考查命题真假的判断,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
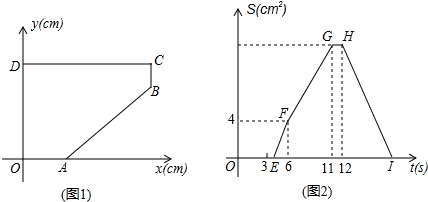
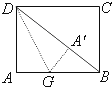 如图,矩形纸片ABCD,AB=8,AD=6,折叠纸片使AD边与对角线BD重合,点A在BD上的落点为点A′,折痕为DG,则AG的长为
如图,矩形纸片ABCD,AB=8,AD=6,折叠纸片使AD边与对角线BD重合,点A在BD上的落点为点A′,折痕为DG,则AG的长为 50个同样大小的立方体木块堆砌成如图所示的形状,现在从前、后、左、右和上面五个方向朝这堆木块喷漆,则有
50个同样大小的立方体木块堆砌成如图所示的形状,现在从前、后、左、右和上面五个方向朝这堆木块喷漆,则有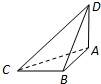 如图,已知球O的球面上四点A,B,C,D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=
如图,已知球O的球面上四点A,B,C,D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=