题目内容
如图,AB是⊙O的直径 ,AC是弦 ,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E.OE交AD于点F.
(1)求证:DE是⊙O的切线;
(2)若 ,求
,求 的值.
的值.
 |
 解:(1)证明:连接OD,∵AD平分∠CAB,
解:(1)证明:连接OD,∵AD平分∠CAB,
∴∠CAD=∠BAD,∵OA=OD,
∴∠BAD=∠ADO,∴∠CAD=∠ODA,
∴OD∥AC,∵DE⊥AC,∴DE⊥OD,
∴直线DE是⊙O的切线.- ---------5分
---------5分
(2)连接BC交OD于G,∵AB是直径,∴∠ACB=90°,

 设AC=4a,AB=5a,由勾股定理得:BC=3a,∴OA=OD=OB=2.5a,
设AC=4a,AB=5a,由勾股定理得:BC=3a,∴OA=OD=OB=2.5a,
∵∠ECG=90°=∠DEC=∠EDG,∴四边形ECGD是矩形,
∵OG为△ABC中位线,∴G为BC中点∴DE=CG=1.5a,∵OD∥AE,OA=OB,
∴CG=BG,∴OG= AC=2a,∴DG=EC=2.5a-2a=0.5a,∴AE=AC+CE=4a+0.5a=4.5a,
AC=2a,∴DG=EC=2.5a-2a=0.5a,∴AE=AC+CE=4a+0.5a=4.5a,
∵OD∥AC,∴△AEF∽△DOF,∴
----------10分

 全优点练单元计划系列答案
全优点练单元计划系列答案某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5.现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
| X | 1 | 2 | 3 | 4 | 5 |
| f | a | 0.2 | 0.45 | b | c |
(1)若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求a,b,c的值;
(2)在(1)的条件下,将等级系数为4的3件日用品记为x1,x2,x3,等级系数为5的2件日用品记为y1,y2,现从x1,x2,x3,y1,y2这5件日用品中任取两件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率.
 :
: 的离心率为
的离心率为 ,右焦点
,右焦点 到直线
到直线 的距离为
的距离为 .
. 的方程;
的方程; (
( )的直线
)的直线 与椭
与椭 圆
圆 两点,
两点, 为椭圆的右顶点,直线
为椭圆的右顶点,直线 分别交直线
分别交直线 于点
于点 ,线段
,线段 的中点为
的中点为 ,记直线
,记直线 的斜率为
的斜率为 ,求证:
,求证: 为定值.
为定值. ,若点
,若点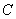 是圆
是圆 上的动点,则
上的动点,则 面积的最小值为 .
面积的最小值为 . (
( )的左焦点
)的左焦点 作
作 轴的垂线交椭圆于点
轴的垂线交椭圆于点 ,
, 为右焦点,若
为右焦点,若 ,则椭圆的离心率为( ).
,则椭圆的离心率为( ). B.
B. C.
C. D.
D.
 ,
, 满足
满足 则
则 的最大值是 .
的最大值是 . .
. ,动点
,动点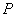 满足
满足 ,则
,则 的最大
的最大