题目内容
5.已知数列{an}的前n项和为Sn,且Sn>0,若a1=6,a2=-2,对于n∈N*,有S2n-12=S2nS2n+2,2S2n+2=S2n-1+S2n+1,则$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{3}}$+$\frac{1}{{S}_{5}}$+…+$\frac{1}{{S}_{2017}}$=$\frac{1009}{2022}$.
分析 由题意有S2n-12=S2nS2n+2,2S2n+2=S2n-1+S2n+1,可得$2\sqrt{{S}_{2n+2}}$=$\sqrt{{S}_{2n}}$+$\sqrt{{S}_{2n+4}}$,利用等差数列通项公式可得$\sqrt{{S}_{2n}}$,可得S2n-1=$\sqrt{{S}_{2n}{S}_{2n+2}}$,再利用“裂项求和”方法即可得出.
解答 解:由题意有S2n-12=S2nS2n+2,2S2n+2=S2n-1+S2n+1,
∴2S2n+2=$\sqrt{{S}_{2n}{S}_{2{n}_{+2}}}$+$\sqrt{{S}_{2n+2}{S}_{2n+4}}$,∴$2\sqrt{{S}_{2n+2}}$=$\sqrt{{S}_{2n}}$+$\sqrt{{S}_{2n+4}}$,
∴数列$\{\sqrt{{S}_{2n}}\}$为等差数列,首项为2,公差为1的等差数列,
∴$\sqrt{{S}_{2n}}$=2+(n-1)=n+1,可得S2n=(1+n)2.∴S2n-1=$\sqrt{{S}_{2n}{S}_{2n+2}}$=(n+1)(n+2).
∴$\frac{1}{{S}_{2n-1}}$=$\frac{1}{n+1}-\frac{1}{n+2}$.
则$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{3}}$+$\frac{1}{{S}_{5}}$+…+$\frac{1}{{S}_{2017}}$=$(\frac{1}{2}-\frac{1}{3})+(\frac{1}{3}-\frac{1}{4})$+…+$(\frac{1}{1010}-\frac{1}{1011})$=$\frac{1}{2}-$$\frac{1}{1011}$=$\frac{1009}{2022}$.
故答案为:$\frac{1009}{2022}$.
点评 本题考查了“裂项求和”方法、等差数列的通项公式、数列递推关系,考查了推理能力与计算能力,属于中档题.

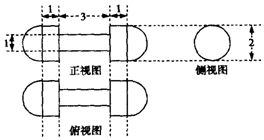 某几何体由三个圆柱和大小相同的两个半球组成,它的三视图如图所示(单位:dm),则该几何体的表面积是( )(侧视图中间有小圆)
某几何体由三个圆柱和大小相同的两个半球组成,它的三视图如图所示(单位:dm),则该几何体的表面积是( )(侧视图中间有小圆)| A. | $\frac{25π}{2}$dm2 | B. | 11πdm2 | C. | $\frac{19π}{2}$dm2 | D. | 9πdm2 |
| A. | {1,2} | B. | {0,1} | C. | {1,2,3} | D. | ∅ |
| A. | {x|$\frac{1}{3}$≤x≤2} | B. | {x|x>2或x≤$\frac{1}{3}$} | C. | {x|$\frac{1}{3}$≤x<2} | D. | {x|x<2} |
| A. | (-∞,-3] | B. | (-∞,-1] | C. | [1,+∞) | D. | [-3,-1] |