题目内容
10.已知集合M={x∈Z|x<3},N={x|ex>1},则M∩N=( )| A. | {1,2} | B. | {0,1} | C. | {1,2,3} | D. | ∅ |
分析 由指数函数的性质求出集合N,由条件和交集的运算求出M∩N.
解答 解:因为集合N={x|ex>1}={x|x>0},
且集合M={x∈Z|x<3},
所以M∩N={1,2},
故选A.
点评 本题考查交集及其运算,以及指数函数的性质,属于基础题.

练习册系列答案
相关题目
20.如图所示的程序框图,其功能是输入x的值,输出相应的y值.若要使输入的x值与输出的y值相等,则这样的x值有( )
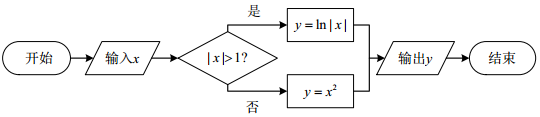

| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
18.已知函数f(x)=cos$\frac{x+2φ}{3}$(φ∈[-π,0])的图象关于原点对称,为了得到函数y=cos($\frac{π}{6}$+$\frac{x}{3}$)的图象,只需把函数f(x)的图象( )
| A. | 向左平移$\frac{2π}{3}$个单位 | B. | 向右平移$\frac{2π}{3}$个单位 | ||
| C. | 向左平移2π个单位 | D. | 向右平移2π个单位 |
15.已知直线l1的斜率为3,直线12经过点(0,5),且l1⊥l2,则直线l2的方程为( )
| A. | x-3y+5=0 | B. | x-3y+15=0 | C. | x+3y-5=0 | D. | x+3y-15=0 |
2.已知抛物线C:y2=4x的焦点是F,过点F的直线与抛物线C相交于P、Q两点,且点Q在第一象限,若$3\overrightarrow{PF}=\overrightarrow{FQ}$,则直线PQ的斜率是( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
19.函数y=xlnx在(0,5)上是( )
| A. | 单调增函数 | |
| B. | 单调减函数 | |
| C. | 在$({0,\frac{1}{e}})$上是增函数,在$({\frac{1}{e},5})$上是减函数 | |
| D. | 在$({0,\frac{1}{e}})$上是减函数,在$({\frac{1}{e},5})$上是增函数 |
20.已知函数y=2sinωx(ω>0)的图象与直线y=-2的相邻的两个公共点之间的距离为$\frac{2π}{3}$,则ω的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{3}{2}$ | C. | 3 | D. | $\frac{2}{3}$ |