题目内容
在三角形ABC中:
(1)若A+B=
,求(1+tanA)(1+tanB)的值.
(2)若lgtanA+lgtanC=2lgtanB,求证:
≤B<
.
(1)若A+B=
| π |
| 4 |
(2)若lgtanA+lgtanC=2lgtanB,求证:
| π |
| 3 |
| π |
| 2 |
考点:两角和与差的正切函数
专题:解三角形
分析:(1)利用正切的两角和公式求得tanA和tanB的关系式,进而化简整理即可求得(1+tanA)(1+tanB)的值.
(2)利用对数的运算法则和已知条件分别求得tanAtanB和tanA+tanB的表达式,利用构造方程根据判别式大于等于0求得tanB的范围,进而求得B的范围.
(2)利用对数的运算法则和已知条件分别求得tanAtanB和tanA+tanB的表达式,利用构造方程根据判别式大于等于0求得tanB的范围,进而求得B的范围.
解答:
解:(1)由A+B=
得tan(A+B)=1即
=1,
即tanA+tanB=1-tanAtanB,
即tanAtanB+tanA+tanB=1,
即tanA(tanB+1)+(tanB+1)=2,
即(tanB+1)(tanA+1)=2,
即(1+tanA)(1+tanB)=2,
(2)由已知得:A,B,C都为锐角,tanA•tanC=tan2B,
∵tanA=-tan(B+C)=-
,
∴tanA+tanB+tanC=tanA•tanB•tanC,
∴tanA+tanC=tan3B-tanB,
∴tanA,tanC是方程x2-(tan3B-tanB)x+tan2B=0的两个实根,
∴△=(tan3B-tanB)2-4tan2B≥0,
即tan2B(tan2B-1)2-4tan2B≥0,
即(tan2B-1)2-4≥0,
即tan2B≥3或tan2B≤-1(舍去),
又因为B为锐角,所以tanB≥
.
所以
≤B<
.
| π |
| 4 |
| tanA+tanB |
| 1-tanAtanB |
即tanA+tanB=1-tanAtanB,
即tanAtanB+tanA+tanB=1,
即tanA(tanB+1)+(tanB+1)=2,
即(tanB+1)(tanA+1)=2,
即(1+tanA)(1+tanB)=2,
(2)由已知得:A,B,C都为锐角,tanA•tanC=tan2B,
∵tanA=-tan(B+C)=-
| tanB+tanC |
| 1-tanB•tanC |
∴tanA+tanB+tanC=tanA•tanB•tanC,
∴tanA+tanC=tan3B-tanB,
∴tanA,tanC是方程x2-(tan3B-tanB)x+tan2B=0的两个实根,
∴△=(tan3B-tanB)2-4tan2B≥0,
即tan2B(tan2B-1)2-4tan2B≥0,
即(tan2B-1)2-4≥0,
即tan2B≥3或tan2B≤-1(舍去),
又因为B为锐角,所以tanB≥
| 3 |
所以
| π |
| 3 |
| π |
| 2 |
点评:本题主要考查了三角函数恒等变换的应用.考查了学生对三角函数基础知识的综合运用.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
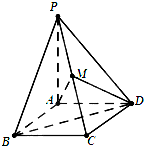 在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥平面ABCD,PA=1,点M是棱PC的中点.
在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥平面ABCD,PA=1,点M是棱PC的中点.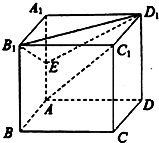 如图,在正方体ABCD-A1B1C1D1中,
如图,在正方体ABCD-A1B1C1D1中, 某次游园的一项活动中,设置了两个中奖方案:
某次游园的一项活动中,设置了两个中奖方案: 已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.点M是棱C1B1上的动点.
已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.点M是棱C1B1上的动点.