题目内容
已知椭圆
+
=1(a>b>0)的离心率为
,设其左、右焦点分别为F1,F2,上顶点为B1,△B1F1F2的面积为2
.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点(2,0)作直线l与椭圆交于A,B两点,O是坐标原点,设
=
+
,是否存在这样的直线l,使四边形OASB的对角线相等(即|
|=|
|)?若存在,求出直线l的方程,若不存在,试说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| 5 |
(Ⅰ)求椭圆的方程;
(Ⅱ)过点(2,0)作直线l与椭圆交于A,B两点,O是坐标原点,设
| OS |
| OA |
| OB |
| OS |
| AB |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知得S△B1F1F2=
×2c×b=2
,e=
=
,由此能求出椭圆方程.
(Ⅱ)若存在l,使得|
|=|
|,则四边形OASB为矩形,设l的方程为y=k(x-2),由
,得(9k2+4)x2-36k2x+36(k2-1)=0,由此利用韦达定理能求出存在直线l:3x-2y-6=0或3x+2y-6=0,使得四边形OASB的对角线相等.
| 1 |
| 2 |
| 5 |
| c |
| a |
| ||
| 3 |
(Ⅱ)若存在l,使得|
| OS |
| AB |
|
解答:
解:(Ⅰ)∵△B1F1F2的面积为2
,∴S△B1F1F2=
×2c×b=2
,
又∵e=
=
,解得c2=5,a2=9,b2=4,
∴椭圆方程为
+
=1.…(5分)
(Ⅱ)∵
=
+
,∴四边形OASB为平行四边形,
若存在l,使得|
|=|
|,则四边形OASB为矩形,
∴
•
=0.(7分)
若l的斜率不存在,直线l的方程为x=2,由
,得
,
∴
•
=
>0,与
•
=0矛盾,故l斜率存在 …(8分)
若l的斜率存在,设l的方程为y=k(x-2),
由
,得(9k2+4)x2-36k2x+36(k2-1)=0,
依题意△>0恒成立,设A(x1,y1),B(x2,y2),
∴x1+x2=
,x1x2=
,①
y1y2=[k(x1-2)][k(x2-2)]=k2[x1x2-2(x1+x2)+4]=-
,②…(11分)
把①、②代入x1x2+y1y2=0,得k=±
,
∴直线l的方程为y=±
(x-2),即3x-2y-6=0或3x+2y-6=0,
综上,存在直线l:3x-2y-6=0或3x+2y-6=0,
使得四边形OASB的对角线相等.…(14分)
| 5 |
| 1 |
| 2 |
| 5 |
又∵e=
| c |
| a |
| ||
| 3 |
∴椭圆方程为
| x2 |
| 9 |
| y2 |
| 4 |
(Ⅱ)∵
| OS |
| OA |
| OB |
若存在l,使得|
| OS |
| AB |
∴
| OA |
| OB |
若l的斜率不存在,直线l的方程为x=2,由
|
|
∴
| OA |
| OB |
| 16 |
| 9 |
| OA |
| OB |
若l的斜率存在,设l的方程为y=k(x-2),
由
|
依题意△>0恒成立,设A(x1,y1),B(x2,y2),
∴x1+x2=
| 36k2 |
| 9k2+4 |
| 36(k2-1) |
| 9k2+4 |
y1y2=[k(x1-2)][k(x2-2)]=k2[x1x2-2(x1+x2)+4]=-
| 20k2 |
| 9k2+4 |
把①、②代入x1x2+y1y2=0,得k=±
| 3 |
| 2 |
∴直线l的方程为y=±
| 3 |
| 2 |
综上,存在直线l:3x-2y-6=0或3x+2y-6=0,
使得四边形OASB的对角线相等.…(14分)
点评:本题考查椭圆方程的求法,考查满足条件的直线方程是否存在的判断与求法,解题时要认真审题,注意椭圆、直线方程、韦达定理,向量等知识点的合理运用.

练习册系列答案
相关题目
在如图的各图中,每个图的两个变量具有线性相关关系的图是( )

| A、①② | B、①③ | C、②④ | D、②③ |
向量
=(1,m),
=(2,-4),若
=λ
(λ为实数),则m的值为( )
| a |
| b |
| a |
| b |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
有一批数量很大的产品,其中次品率为3%,从中任取产品进行不放回抽查,若取到正品则停止;若取到次品则继续,最多取3次.设X表示取出产品的个数,则P(X=3)=( )
| A、0.03×0.97 |
| B、0.972×0.03 |
| C、0.032×0.97+0.033 |
| D、0.972×0.03+0.033 |
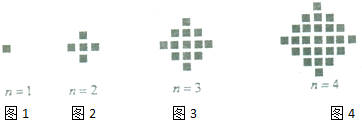 图为某少数民族最常见的四个刺绣图案,这些图案都是小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
图为某少数民族最常见的四个刺绣图案,这些图案都是小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.