题目内容
若x>y>0,则下列不等式正确的是( )
| A、3x<3y | ||||
B、
| ||||
| C、lnx<lny | ||||
D、(
|
考点:对数函数的单调性与特殊点
专题:函数的性质及应用
分析:由已知中x>y>0,结合指数函数的单调性,对数函数的单调性,不等式的基本性质,逐一分析四个答案的正误,可得结论.
解答:
解:∵x>y>0,
y=3x为增函数,故3x>3y,故A错误;
不等式x>y两边同除xy得:
<
,故B正确;
y=lnx为增函数,故lnx>lny,故C错误;
y=(
)x为减函数,故(
)x<(
)y,故D错误;
故选:B
y=3x为增函数,故3x>3y,故A错误;
不等式x>y两边同除xy得:
| 1 |
| x |
| 1 |
| y |
y=lnx为增函数,故lnx>lny,故C错误;
y=(
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
故选:B
点评:本题考查的知识点是指数函数的单调性和对数函数的单调性,难度不大,属于基础题.

练习册系列答案
相关题目
某市对10000名中学生的数学成绩(满分100分)进行抽样统计,发现他们近似服从正态分布N~(70,102),若90分以上者有230人,则这10000名学生中分数在50分到90分之间的人数约有( )
| A、7140人 | B、230人 |
| C、9540人 | D、4770人 |
如果袋中有6个红球,4个白球,从中任取1球,记住颜色后放回,连续摸取4次,设ξ为取得红球的次数,则Eξ为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
经过点A(1,0),B(0,1)的直线方程为( )
| A、y=x+1 |
| B、y=x-1 |
| C、y=-x+1 |
| D、y=-x-1 |
已知等比数列{an}的各项都是正数,且5a1,
a3,4a2成等差数列,则
=( )
| 1 |
| 2 |
| a2n+1+a2n+2 |
| a1+a2 |
| A、-1 |
| B、1 |
| C、52n |
| D、52n-1 |
已知实数x,y满足
,则x+y的最小值为( )
|
| A、2 | B、3 | C、4 | D、5 |
阅读如图所示的程序框图,若输入的k=6,则输出的值S是( )


| A、63 | B、64 |
| C、127 | D、128 |
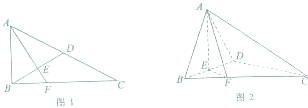 如图1,在Rt△ABC中,∠ACB=30°,∠ABC=90°,D为AC中点,AE⊥BD于E,延长AE交BC于F,将△ABD沿BD折起,使平面ABD⊥平面BCD,如图2所示.
如图1,在Rt△ABC中,∠ACB=30°,∠ABC=90°,D为AC中点,AE⊥BD于E,延长AE交BC于F,将△ABD沿BD折起,使平面ABD⊥平面BCD,如图2所示.