题目内容
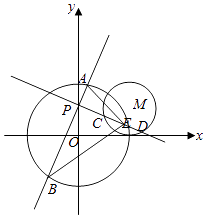
【题目】在直角坐标系中,椭圆C1: ![]() 的左、右焦点分别为F1 , F2 , 其中F2也是抛物线C2:y2=4x的焦点,点P为C1与C2在第一象限的交点,且
的左、右焦点分别为F1 , F2 , 其中F2也是抛物线C2:y2=4x的焦点,点P为C1与C2在第一象限的交点,且 ![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)过F2且与坐标轴不垂直的直线交椭圆于M、N两点,若线段OF2上存在定点T(t,0)使得以TM、TN为邻边的四边形是菱形,求t的取值范围.
【答案】解:(Ⅰ)抛物线y2=4x的焦点为(1,0), ![]() ,∴
,∴ ![]() ,
,
∴ ![]() ,∴
,∴ ![]() ,
,
又F2(1,0),∴F1(﹣1,0),
∴ ![]() ,∴a=2,
,∴a=2,
又∵c=1,∴b2=a2﹣c2=3,
∴椭圆方程是: ![]() .
.
(Ⅱ)设MN中点为D(x0,y0),∵以TM、TN为邻边的四边形是菱形,
∴TD⊥MN,
设直线MN的方程为x=my+1,
联立 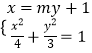 ,整理得(3m2+4)y2+6my﹣9=0,
,整理得(3m2+4)y2+6my﹣9=0,
∵F2在椭圆内,∴△>0恒成立,
∴ ![]() ,
,
∴ ![]() ,∴
,∴ ![]() ,
,
∴kTDkMN=﹣1,即 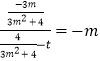 ,
,
整理得 ![]() ,
,
∵m2>0,∴3m2+4∈(4,+∞),∴ ![]() ,
,
∴t的取值范围是 ![]() .
.
【解析】(Ⅰ)根据题意由已知可列出方程组求出a、b的值,因此能求出椭圆的方程。(Ⅱ)设出中点的坐标根据题意的垂直关系可设出直线的方程再联立椭圆的方程消去x得到关于y的一元二次函数,利用韦达定理、根的判别式、两直线的垂直的关系再结合已知条件即可求出t的取值范围。

练习册系列答案
相关题目