Question

【题目】如图，在四棱柱ABCD﹣A1B1C1D1中，侧面ADD1A1⊥底面ABCD，D1A=D1D= ，底面ABCD为直角梯形，其中BC∥AD，AB⊥AD，AD=2AB=2BC=2，O为AD中点．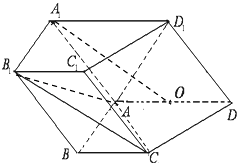

（Ⅰ）求证：A1O∥平面AB1C；
（Ⅱ）求锐二面角A﹣C1D1﹣C的余弦值．

Answer 1

【答案】（Ⅰ）证明：如图，连接CO，AC，

则四边形ABCO为正方形，

∴OC=AB=A1B1，且OC∥AB∥A1B1

∴四边形A1B1CO为平行四边形，

∴A1O∥B1C，

又∵A1O平面AB1C，B1C平面AB1C，

∴A1O∥平面AB1C．…

（Ⅱ）∵D1A=D1D，O为AD的中点，

∴D1O⊥AD，又侧面ADD1A1⊥底面ABCD，

∴D1O⊥底面ABCD，…

以O为原点，OC，OD，OD1所在直线分别为x轴，y轴，Z轴，

建立如图所示的坐标系，

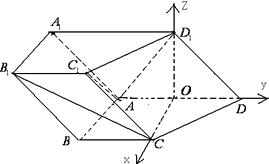
由题意得：C（1，0，0），D（0，1，0），

D1（0，0，1），A（0，﹣1，0），…

∴ ， =（0，﹣1，1），

=（0，﹣1，﹣1）， =（1，﹣1，0），

设 为平面CDD1C1的一个法向量，

则 ，∴ ，

令Z=1，则y=1，x=1，∴ ，…

设 为平面AC1D1的一个法向量，

则 ，∴ ，令Z1=1，

则y1=﹣1，x1=﹣1，∴ ，

∴ ，

∴所求锐二面角A﹣C1D1﹣C的余弦值为 ．…

【解析】（1）连接CO，AC易证为平行四边形，由此可证∥平面;（2）以O为坐标原点，OC，OD，为x，y，z轴建立空间直角坐标系，利用法向量求出锐二面角。
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点，需要掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行才能正确解答此题．