题目内容
15．若l，m，n为空间的三条直线，l⊥m，m⊥n，则l与n的位置关系为平行或相交或异面．分析 根据直线l，n的位置可能进行讨论分析，得到正确答案．
解答 解：如果直线l，n在同一个平面内不相交，则直线l∥n；如果相交，也可以满足l⊥m，m⊥n，如墙角的三条棱；
如果不在同一个平面内，也可以满足l⊥m，m⊥n；
所以l与n的位置关系为平行或相交或异面；
故答案为；平行或相交或异面．
点评 本题考查了空间直线的位置关系的判断；考查学生的空间想象能力；注意问题的全面性．
练习册系列答案
小夫子全能检测系列答案
相关题目
10．已知正数a，b满足ab≥a+b+8则a+b的最小值为（ ）
| A． | 4 | B． | 8 | C． | 16 | D． | 32 |
20．
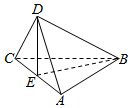已知正方形ABCD的对角线AC与BD相交于E点，将△ACD沿对角线折起，使得平面ABC⊥平面ADC（如图），则下列命题中正确的是（ ）
已知正方形ABCD的对角线AC与BD相交于E点，将△ACD沿对角线折起，使得平面ABC⊥平面ADC（如图），则下列命题中正确的是（ ）| A． | 直线AB⊥直线CD，且直线AC⊥直线BD | |
| B． | 直线AB⊥平面BCD，且直线AC⊥平面BDE | |
| C． | 平面ABC⊥平面BDE，且平面ACD⊥BDE | |
| D． | 平面ABD⊥平面BCD，且平面ACD⊥平面BDE |