题目内容
19．不等式组$\left\{\begin{array}{l}x≥0\\ y≤x\\ 2x+y-9≤0\end{array}\right.$所表示的平面区域为D．若直线y=a（x+1）与区域D有公共点，则实数a的取值范围是$（-∞，\frac{3}{4}]$．分析 作出不等式组对应的平面区域，利用目标函数的几何意义，利用数形结合进行求解即可．
解答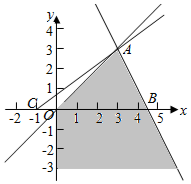 
解：作出不等式组对应的平面区域图示：
因为y=a（x+1）过定点C（-1，0）．
当a≤0时，直线y=a（x+1）与区域D有公共点，满足条件．
当a＞0时，当直线y=a（x+1）过点A时，由公共点，
由$\left\{\begin{array}{l}{y=x}\\{2x+y-9=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$，即A（3，3），
代入y=a（x+1）得4a=3，a=$\frac{3}{4}$，
又因为直线y=a（x+1）与平面区域D有公共点．
此时0＜a≤$\frac{3}{4}$．
综上所述，a≤$\frac{3}{4}$．
故答案为：$（-∞，\frac{3}{4}]$．
点评 本题主要考查线性规划的应用，利用目标函数的几何意义，结合数形结合的数学思想是解决此类问题的基本方法．
练习册系列答案
名校课堂系列答案
相关题目
9．已知函数f（x）=$\left\{\begin{array}{l}|lo{g}_{3}x|，0＜x＜3\\-cos（\frac{π}{3}x），3≤x≤9\end{array}\right.$，若存在实数x1，x2，x3，x4，当x1＜x2＜x3＜x4时满足f（x1）=f（x2）=f（x3）=f（x4），则x1•x2•x3•x4的取值范围是（ ）
| A． | （7，$\frac{29}{4}$） | B． | （21，$\frac{135}{4}$） | C． | [27，30） | D． | （27，$\frac{135}{4}$） |
10．下列有关命题的说法错误的是（ ）
| A． | 函数f（x）=sinxcosx的最小正周期为π | |
| B． | 函数$f（x）=lnx+\frac{1}{2}x-2$在区间（2，3）内有零点 | |
| C． | 已知函数$f（x）={log_a}（{x^2}-2x+2）$，若$f（\frac{1}{2}）＞0$，则0＜a＜1 | |
| D． | 在某项测量中，测量结果ξ服从正态分布N（2，σ2）（σ＞0）．若ξ在（-∞，1）内取值的概率为0.1，则ξ在（2，3）内取值的概率为0.4 |
4．某班倡议假期每位学生至少阅读一本名著，为了解学生的阅读情况，对该班所有学生进行了调查．调查结果如表：
（Ⅰ）试根据上述数据，求这个班级女生阅读名著的平均本数；
（Ⅱ）若从阅读5本名著的学生中任选2人交流读书心得，求选到男生和女生各1人的概率；
（Ⅲ）试判断该班男生阅读名著本数的方差${s_1}^2$与女生阅读名著本数的方差${s_2}^2$的大小
（只需写出结论）．（注：方差${s^2}=\frac{1}{n}[{（{x_1}-\bar x）^2}+{（{x_2}-\bar x）^2}+…+{（{x_n}-\bar x）^2}]$，其中$\overline x$为x1x2，…xn的平均数）
| 阅读名著的本数 | 1 | 2 | 3 | 4 | 5 |
| 男生人数 | 3 | 1 | 2 | 1 | 3 |
| 女生人数 | 1 | 3 | 3 | 1 | 2 |
（Ⅱ）若从阅读5本名著的学生中任选2人交流读书心得，求选到男生和女生各1人的概率；
（Ⅲ）试判断该班男生阅读名著本数的方差${s_1}^2$与女生阅读名著本数的方差${s_2}^2$的大小
（只需写出结论）．（注：方差${s^2}=\frac{1}{n}[{（{x_1}-\bar x）^2}+{（{x_2}-\bar x）^2}+…+{（{x_n}-\bar x）^2}]$，其中$\overline x$为x1x2，…xn的平均数）
8．设复数z满足（1+i）z=2i，则z的共轭复数$\overline{z}$=（ ）
| A． | -1-i | B． | -1-i | C． | 1+i | D． | 1-i |