题目内容
已知非负实数a,b满足a+b≤1,则关于x的一元二次方程x2+ax+b2=0有实根的概率是 .
考点:古典概型及其概率计算公式
专题:概率与统计
分析:关于x的一元二次方程x2+ax+b2=0有实根,必有a2≥4b2,即a≥2b或a≤-2b,进而分析非负实数a,b满足a+b≤1表示的区域及其面积,由几何概型公式计算可得答案.
解答:
解:关于x的一元二次方程x2+ax+b2=0有实根,必有a2≥4b2,即a≥2b或a≤-2b,
而非负实数a,b满足a+b≤1,表示如图的三角形区域△OAB,其面积为
×1×1=
,
∴满足关于x的一元二次方程x2+ax+b2=0有实根且落在三角形区域内的面积为
×1×
=
,
∴关于x的一元二次方程x2+ax+b2=0有实根的概率是=
=
.
故答案为:
而非负实数a,b满足a+b≤1,表示如图的三角形区域△OAB,其面积为
| 1 |
| 2 |
| 1 |
| 2 |
∴满足关于x的一元二次方程x2+ax+b2=0有实根且落在三角形区域内的面积为
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
∴关于x的一元二次方程x2+ax+b2=0有实根的概率是=
| ||
|
| 1 |
| 3 |

故答案为:
| 1 |
| 3 |
点评:本题考查几何概型的计算,关键是要找出(a,b)对应图形的面积,及满足条件“关于x的一元二次方程x2+ax+b2=0有实根”的点对应的图形的面积,然后再结合几何概型的计算公式进行求解.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
函数y=x-lnx的单调递增区间是( )
| A、(0,1) |
| B、(-∞,1) |
| C、(1,2) |
| D、(1,+∞) |
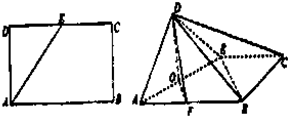 已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△ADE折起,使平面ADE上平面ABCE,点O、F分别是AE、AB的中点.
已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△ADE折起,使平面ADE上平面ABCE,点O、F分别是AE、AB的中点.