题目内容
已知函数f（x）=
x3-（a-1）x2+b2x，其中a，b为常数．若任取a∈[0，4]，b∈[0，3]，则函数f（x）在R上是增函数的概率是 ．
| 1 |
| 3 |
考点：利用导数研究函数的单调性,几何概型
专题：导数的综合应用,概率与统计
分析：这是一个几何概型问题，我们可以先画出a∈[0，4]，b∈[0，3]，对应的平面区域的面积，然后再求出满足条件函数f（x）在R上是增函数时对应的平面区域的面积，计算出对应的面积后，代入几何概型公式即可得到答案．
解答：
解：f'（x）=x2-2（a-1）x+b2
若函数f（x）在R上是增函数，则对于任意x∈R，f'（x）≥0恒成立．
所以，△=4（a-1）2-4b2≤0，即（a+b-1）（a-b-1）≤0
设“f（x）在R上是增函数”为事件A，则事件A对应的区域为{（a，b）|（a+b-1）（a-b-1）≤0}
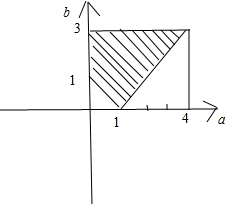
全部试验结果构成的区域{Ω=（a，b）|0≤a≤4，0≤b≤3}，如图．
所以，P（A）=
=
=
．
故函数f（x）在R上是增函数的概率为
，
故答案为
．
解：f'（x）=x2-2（a-1）x+b2若函数f（x）在R上是增函数，则对于任意x∈R，f'（x）≥0恒成立．
所以，△=4（a-1）2-4b2≤0，即（a+b-1）（a-b-1）≤0
设“f（x）在R上是增函数”为事件A，则事件A对应的区域为{（a，b）|（a+b-1）（a-b-1）≤0}
全部试验结果构成的区域{Ω=（a，b）|0≤a≤4，0≤b≤3}，如图．
所以，P（A）=
| s阴影 |
| sΩ |
3×4-
| ||||
| 3×4 |
| 7 |
| 12 |
故函数f（x）在R上是增函数的概率为
| 7 |
| 12 |
故答案为
| 7 |
| 12 |
点评：这是一个几何概型的概率题，本题的关键是找到事件A对应的区域和试验的全部结果，根据几何概型公式就可以算出结果．
练习册系列答案
名校课堂系列答案
相关题目
若一个空间几何体的三视图正视图和侧视图都是半径为1的半圆，俯视图是半径为1的圆，则该几何体的体积等于（ ）
| A、4π | ||
B、
| ||
C、
| ||
D、
|