题目内容
已知函数f(x)对定义域R内的任意x都有f(x)=f(4-x),且当x≠2时,其导数f′(x)满足xf′(x)>2f′(x),若2<a<4,则( )
A.f(2a)<f(3)<f(log2a)
B.f(3)<f(log2a)<f(2a)
C.f(log2a)<f(3)<f(2a)
D.f(log2a)<f(2a)<f(3)
C
[解析] 由f(x)=f(4-x)知函数f(x)的图象关于x=2对称,由x·f′(x)>2f′(x)得(x-2)·f′(x)>0,即当x>2时,f′(x)>0,f(x)单调递增;当x<2时,f′(x)<0,f(x)单调递减.∵2<a<4,∴2a>4>3,1<log2a<2,∴f(2a)>f(3)>f(log2a).故选C.

练习册系列答案
相关题目
 中,
中, ,则点
,则点 到平面
到平面 的距离为
的距离为 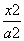 +
+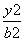 =1(a>b>0)上的任意一点,若∠PF1F2=α,∠PF2F1=β,且cos α=
=1(a>b>0)上的任意一点,若∠PF1F2=α,∠PF2F1=β,且cos α=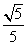 ,sin(α+β)=
,sin(α+β)=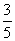 ,则此椭圆的离心率为________.
,则此椭圆的离心率为________.

 dx=3+ln 2(a>1),则a的值为( )
dx=3+ln 2(a>1),则a的值为( ) },那么由函数y=f(x)的图象、x轴、直线x=
},那么由函数y=f(x)的图象、x轴、直线x=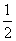 和直线x=4所围成的封闭图形的面积为________.
和直线x=4所围成的封闭图形的面积为________. 满足
满足 ,且
,且 ,则向量
,则向量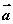 与
与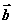 的夹角是( )
的夹角是( ) 的前
的前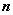 项和
项和 满足:
满足: ,等比数列
,等比数列 的前
的前 ,公
,公 ,且
,且 .
. 的前
的前 ,求证:
,求证:
 上一点,P到直线
上一点,P到直线 的距离与原点到这条直线的距离相等,则点P的坐标是
的距离与原点到这条直线的距离相等,则点P的坐标是