题目内容
19.平面直角坐标系xOy中,直线y=5与抛物线C:x2=2py(p>0)交于点A,B,若△OAB的垂心为C的焦点,则p的值为2.分析 将y=5代入抛物线的方程,可得A,B的坐标,求得抛物线的焦点坐标,再由垂心的性质可得AF⊥OB,即有kAF•kOB=-1,再由斜率公式,解方程即可得到p的值.
解答 解:由y=5代入抛物线C:x2=2py可得,
A(-$\sqrt{10P}$,5),B($\sqrt{10P}$,5),
由抛物线x2=2py可得焦点为F(0,$\frac{p}{2}$),
由△OAB的垂心为C的焦点,可得
AF⊥OB,即有kAF•kOB=-1,
即为$\frac{5-\frac{p}{2}}{-\sqrt{10p}}$•$\frac{5}{\sqrt{10p}}$=-1,
解方程可得p=2.
故答案为:2.
点评 本题考查抛物线的方程和性质,考查三角形的垂心的性质,同时考查直线的斜率公式的运用,属于中档题.

练习册系列答案
相关题目
9.$在△ABC中,|{\overrightarrow{BC}}|=8,|{\overrightarrow{CA}}|=6,\overrightarrow{BA}•\overrightarrow{CA}$=60,则∠C=( )
| A. | 60° | B. | 30° | C. | 150° | D. | 120° |
11.若关于x的不等式xlnx+x-kx+3k>0对任意x>1恒成立,则整数k的最大值是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
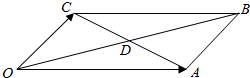 在下图平行四边形?OABC中,两对角线OB与AC相交于点D,若$\overrightarrow{OA}$=(3,1),$\overrightarrow{OC}$=(1,3),则向量$\overrightarrow{OD}$的坐标是(2,2).
在下图平行四边形?OABC中,两对角线OB与AC相交于点D,若$\overrightarrow{OA}$=(3,1),$\overrightarrow{OC}$=(1,3),则向量$\overrightarrow{OD}$的坐标是(2,2).