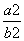题目内容
在平面直角坐标系xOy中,已知椭圆C: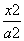 +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= 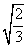 ,且椭圆C上的点到Q(0,2)的距离的最大值为3.
,且椭圆C上的点到Q(0,2)的距离的最大值为3.
(1)求椭圆C的方程;
(2)在椭圆C上,是否存在点M(m,n),使得直线l:mx+ny=1与圆O:x2+y2=1相交于不同的两点A,B,且△OAB的面积最大?若存在,求出点M的坐标及相对应的△OAB的面积;若不存在,请说明理由.
(1)因为e= 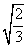 =
=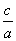 =
= ,
,
所以a2=3b2,即椭圆C的方程可写为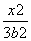 +
+ =1. (2分)
=1. (2分)
设P(x,y)为椭圆C上任意给定的一点,
则d=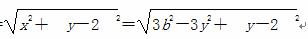 =
=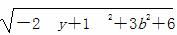 (-b≤y≤b). (3分)
(-b≤y≤b). (3分)
当-b≤-1,即b≥1,dmax= =3得b=1;
=3得b=1;
当-b>-1,即b<1,dmax= =3得b=1(舍).
=3得b=1(舍).
∴b=1,a=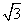 , (5分)
, (5分)
故所求椭圆C的方程为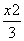 +y2=1. (6分)
+y2=1. (6分)
(2)存在点M满足要求,使△OAB的面积最大. (7分)
假设存在满足条件的点M,因为直线l:mx+ny=1与
圆O:x2+y2=1相交于不同的两点A,B,
则圆心O到l的距离d=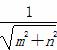 <1. (8分)
<1. (8分)
因为点M(m,n)在椭圆C上,所以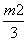 +n2=1<m2+n2,
+n2=1<m2+n2,
于是0<m2≤3.
因为|AB|=2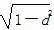 =2
=2 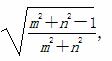 , (10分)
, (10分)
所以S△OAB=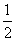 ·|AB|·d=
·|AB|·d=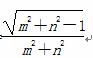
=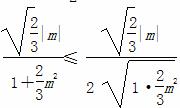 =
=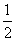 ,
,
当且仅当1=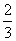 m2时等号成立,所以m2=
m2时等号成立,所以m2=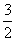 ∈(0,3].
∈(0,3].
因此当m=± ,n=±
,n=±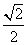 时等号成立. (12分)
时等号成立. (12分)
所以满足要求的点M的坐标为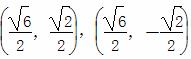
 此时对应的三角形的面积均达到最大值
此时对应的三角形的面积均达到最大值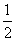 .
.

 备战中考寒假系列答案
备战中考寒假系列答案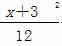 -
-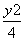 =1 B.
=1 B. 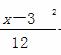 +
+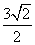 .设P为直线l上的点,过点P作抛物线C的两条切线PA,PB,其中A,B为切点.
.设P为直线l上的点,过点P作抛物线C的两条切线PA,PB,其中A,B为切点.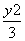 =1的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则
=1的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则 的最小值为( ).
的最小值为( ). C.1 D.0
C.1 D.0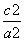 B.-
B.-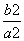 C.-
C.-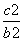 D.-
D.-