题目内容
平面直角坐标系xOy中,过椭圆M: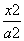 +
+ =1(a>b>0)右焦点的直线x+y-
=1(a>b>0)右焦点的直线x+y-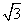 =0交M于A,B两点,P为AB的中点,且OP的斜率为
=0交M于A,B两点,P为AB的中点,且OP的斜率为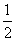 .
.
(1)求M的方程;
(2)C,D为M上的两点,若四边形ACBD的对角线CD⊥AB,求四边形ABCD面积的最大值.
解 (1)设A(x1,y1),B(x2,y2),P0(x0,y0),
则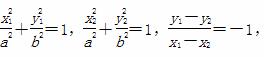
由此可得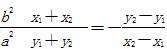 =1.
=1.
因为P为AB的中点,且OP的斜率为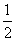 ,
,
所以x1+x2=2x0,y1+y2=2y0,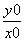 =
=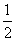 .
.
所以y0=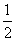 x0,即y1+y2=
x0,即y1+y2=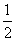 (x1+x2).
(x1+x2).
所以a2=2b2,
又由题意知,M的右焦点为(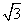 ,0),故a2-b2=3.
,0),故a2-b2=3.
所以a2=6,b2=3.
所以M的方程为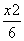 +
+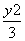 =1.
=1.
(2)将x+y-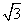 =0代入
=0代入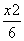 +
+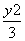 =1,
=1,
解得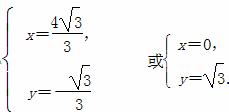 所以可得|AB|=
所以可得|AB|=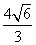 ;
;
由题意可设直线CD方程为y=x+m,
所以设C(x3,y3),D(x4,y4),
将y=x+m代入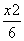 +
+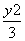 =1得3x2+4mx+2m2-6=0,则|CD|=
=1得3x2+4mx+2m2-6=0,则|CD|=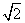
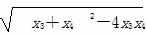 =
=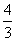
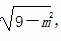 ,
,
又因为Δ=16m2-12(2m2-6)>0,即-3<m<3,
所以当m=0时,|CD|取得最大值4,
所以四边形ACBD面积的最大值为
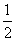 |AB|·|CD|=
|AB|·|CD|=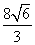 .
.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
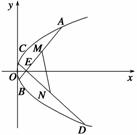
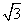 x与双曲线C:
x与双曲线C: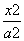 -
-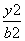 =1(a>0,b>0)左右两支分别交于M、N两点,F是双曲线C的右焦点,O是坐标原点,若|FO|=|MO|,则双曲线的离心率等于( ).
=1(a>0,b>0)左右两支分别交于M、N两点,F是双曲线C的右焦点,O是坐标原点,若|FO|=|MO|,则双曲线的离心率等于( ).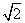 B.
B. -
-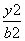 =1(a>0,b>0)有相同的焦点F,点A是两曲线的交点,且AF⊥x轴,则双曲线的离心率为( ).
=1(a>0,b>0)有相同的焦点F,点A是两曲线的交点,且AF⊥x轴,则双曲线的离心率为( ).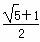 B.
B. +1 C.
+1 C. +1 D.
+1 D. 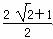
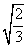 ,且椭圆C上的点到Q(0,2)的距离的最大值为3.
,且椭圆C上的点到Q(0,2)的距离的最大值为3. ”的单调递增函数是( )
”的单调递增函数是( ) (B)
(B) (C)
(C)
 1/2 (D)
1/2 (D)

 +
+ ≥2成立的条件有( )
≥2成立的条件有( )