题目内容
已知P(0,2)已知直线l:y=kx+b与圆C:x2+y2=4相交与A,B两点,当|PA|•|PB|=4时,试证明点P到直线l的距离为定值.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:当|PA|•|PB|=4时,用特殊点法求出点P到直线l的距离,再证明点P到直线l的距离是定值即可.
解答:
解: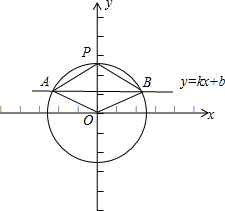 当|PA|•|PB|=4时,用特殊点法求出点P到直线l的距离为1,如图所示;
当|PA|•|PB|=4时,用特殊点法求出点P到直线l的距离为1,如图所示;
现在证明1是点P(0,2)到直线l:y=kx+b=0的距离的定值;
由点P(0,2)到直线l:y=kx+b=0的距离是1,
∴
=1,
∴(b-2)2=1+k2,
∴k2=b2-4b+3;
设A(x1,y1),B(x2,y2),
由直线l:y=kx+b与圆C:x2+y2=4,消去y,
得x2+(kx+b)2=4
即(k2+1)x2+2kbx+b2-4=0;
∴x1+x2=-
,x1x2=
;
∵|PA|•|PB|=4,∴
•
=4,
∴(x12+y12-4y1+4)(x22+y22-4y2+4)=16,
∴(4-4y1+4)(4-4y2+4)=16,
∴(2-y1)(2-y2)=1,
∴y1y2-2(y1+y2)+3=0;
即(kx1+b)(kx2+b)-2(kx1+b+kx2+b)+3=0,
k2x1x2+(kb-2k)(x1+x2)-4b+3=0,
∴k2•
+(kb-2b)•(-
)-4b+3=0,
化简得k2=b2-4b+3;
即证点P到直线l的距离为定值,且定值为1.
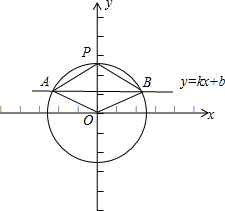 当|PA|•|PB|=4时,用特殊点法求出点P到直线l的距离为1,如图所示;
当|PA|•|PB|=4时,用特殊点法求出点P到直线l的距离为1,如图所示;现在证明1是点P(0,2)到直线l:y=kx+b=0的距离的定值;
由点P(0,2)到直线l:y=kx+b=0的距离是1,
∴
| |-2+b| | ||
|
∴(b-2)2=1+k2,
∴k2=b2-4b+3;
设A(x1,y1),B(x2,y2),
由直线l:y=kx+b与圆C:x2+y2=4,消去y,
得x2+(kx+b)2=4
即(k2+1)x2+2kbx+b2-4=0;
∴x1+x2=-
| 2kb |
| k2+1 |
| b2-4 |
| k2+1 |
∵|PA|•|PB|=4,∴
| x12+(y1-2)2 |
| x22+(y2-2)2 |
∴(x12+y12-4y1+4)(x22+y22-4y2+4)=16,
∴(4-4y1+4)(4-4y2+4)=16,
∴(2-y1)(2-y2)=1,
∴y1y2-2(y1+y2)+3=0;
即(kx1+b)(kx2+b)-2(kx1+b+kx2+b)+3=0,
k2x1x2+(kb-2k)(x1+x2)-4b+3=0,
∴k2•
| b2-4 |
| k2+1 |
| 2kb |
| k2+1 |
化简得k2=b2-4b+3;
即证点P到直线l的距离为定值,且定值为1.
点评:本题考查了直线与圆的应用问题,考查了定值的应用问题,用特殊点法求出点P到直线l的距离,再证明点P到直线l的距离是定值是关键.

练习册系列答案
相关题目
先将函数f(x)=sinxcosx的图象向左平移
个长度单位,再保持所有点的纵坐标不变,横坐标压缩为原来的
,得到函数g(x)的图象,则使g(x)为增函数的一个区间是( )
| π |
| 4 |
| 1 |
| 2 |
A、(
| ||||
B、(
| ||||
C、(0,
| ||||
| D、(-π,0) |
已知各项均为实数的数列{an}为等比数列,且满足a1+a2=12,a2a4=1则a1=( )
A、9或
| ||||
B、
| ||||
C、
| ||||
| D、9或16 |
若函数f(x)(x∈R)是奇函数,则( )
| A、函数f(x2)是奇函数 |
| B、函数[f(x)]2是奇函数 |
| C、函数f(x)•x2是奇函数 |
| D、函数f(x)+x2是奇函数 |
 某工厂对100件新产品的尺寸(单位:cm)进行检测,所得数据均在[5,25]中,其频率分布直方图如图,则在这100件新产品中,有
某工厂对100件新产品的尺寸(单位:cm)进行检测,所得数据均在[5,25]中,其频率分布直方图如图,则在这100件新产品中,有