题目内容
13.设函数f(x)为偶函数,当x∈(0,+∞)时,f(x)=log2x,则f($-\sqrt{2}$)=$\frac{1}{2}$.分析 直接利用函数的奇偶性以及函数的解析式求解即可.
解答 解:函数f(x)为偶函数,当x∈(0,+∞)时,f(x)=log2x,
则f($-\sqrt{2}$)=f($\sqrt{2}$)=log2$\sqrt{2}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查函数的奇偶性以及函数的解析式的应用,考查计算能力.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
8.执行如图所示的程序框图,输出$s=\frac{2015}{2016}$.那么判断框内应填( )
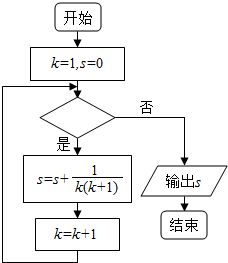

| A. | k≤2015 | B. | k≤2016 | C. | k≥2015 | D. | k≥2016 |
18.设集合A={x|y=$\sqrt{1-{x}^{2}}$},B={y|y=$\sqrt{1-{x}^{2}}$},则A∩B=( )
| A. | {(-1,1)} | B. | {(0,1)} | C. | [-1,1] | D. | [0,1] |
5.若点P是曲线y2=4x上的一个动点,则点P到点A(0,1)的距离与点P到y轴的距离之和的最小值为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{2}-1$ | C. | $\sqrt{2}+1$ | D. | 2 |
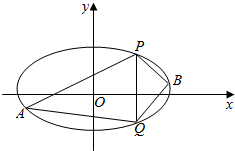 已知椭圆C的中心在坐标原点,离心率为$\frac{1}{2}$,且它的短轴端点恰好是双曲线$\frac{y^2}{8}-\frac{x^2}{4}=1$的焦点.
已知椭圆C的中心在坐标原点,离心率为$\frac{1}{2}$,且它的短轴端点恰好是双曲线$\frac{y^2}{8}-\frac{x^2}{4}=1$的焦点.