题目内容

18．设集合A={x|y=$\sqrt{1-{x}^{2}}$}，B={y|y=$\sqrt{1-{x}^{2}}$}，则A∩B=（　　）
A．{（-1，1）}B．{（0，1）}C．[-1，1]D．[0，1]

分析 求出y=$\sqrt{1-{x}^{2}}$中x的范围确定出A，求出y的范围确定出B，找出两集合的交集即可．

解答 解：由A中y=$\sqrt{1-{x}^{2}}$，得到1-x2≥0，
解得：-1≤x≤1，即A=[-1，1]，
由B中y=$\sqrt{1-{x}^{2}}$，得到0≤y≤1，即B=[0，1]，
则A∩B=[0，1]，
故选：D．

点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．

练习册系列答案
相关题目
8．中心在坐标原点O，焦点在坐标轴上的椭圆E经过两点$R（{-\frac{{\sqrt{3}}}{2}，-\frac{{\sqrt{6}}}{2}}），Q（{\frac{3}{2}，\frac{{\sqrt{2}}}{2}}）$．分别过椭圆E的焦点F1、F2的动直线l1，l2相交于P点，与椭圆E分别交于A、B与C、D不同四点，直线OA、OB、OC、OD的斜率k1、k2、k3、k4满足k1+k2=k3+k4．
（1）求椭圆E的方程；
（2）是否存在定点M、N，使得|PM|+|PN|为定值．若存在，求出M、N点坐标并求出此定值，若不存在，说明理由．
9．若集合U={1，2，3，4，5}，A={1，2，3}，B={2，3，4}，则∁U（A∪B）=（　　）
A．{5}B．{2}C．{1，2，3，4}D．{1，3，4，5}
6．如图，在正四棱柱ABCD-A1B1C1D1中，E，F分别是AB1，BC1的中点，则以下结论中不成立的是（　　）
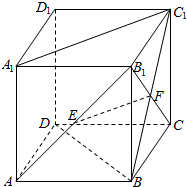
A．EF与BB1垂直B．EF与BD垂直C．EF与CD异面D．EF与A1C1异面
13．设函数f（x）为偶函数，当x∈（0，+∞）时，f（x）=log2x，则f（$-\sqrt{2}$）=$\frac{1}{2}$．
3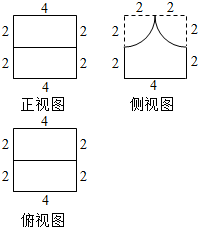．某几何体的三视图如图所示（其中侧视图为正方形上半部分在两个角上各截去四分之一圆），则该几何体的表面积为（　　）
A．48+4πB．48+8πC．64+4πD．64+8π
10．已知函数f（x）=$\left\{\begin{array}{l}{-{x}^{2}-x（x≥0）}\\{{x}^{2}-x（x＜0）}\end{array}\right.$，对于任意x∈[1，+∞），不等式f（a2-ex-1）＞f（2x2-2a）恒成立，则实数a的取值范围为（-3，1）．
7．函数f（x）=x2-1（2＜x＜3）的反函数为（　　）
A．f-1（x）=$\sqrt{x-1}$（3＜x＜8）B．f-1（x）=$\sqrt{x+1}$（3＜x＜8）C．f-1（x）=$\sqrt{x-1}$（4＜x＜9）D．f-1（x）=$\sqrt{x+1}$（4＜x＜9）
8．已知函数y=f（x-1）是奇函数，且f（2）=1，则f（-4）=（　　）
A．1B．3C．-1D．-3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网