题目内容
 已知函数y=f(x),x∈[-2,2],当x∈[0,2]的图象,且y=f(x)是偶函数.
已知函数y=f(x),x∈[-2,2],当x∈[0,2]的图象,且y=f(x)是偶函数.(1)求y=f(x),x∈[-2,2];
(2)求单调区间、最值;
(3)求f(x)<0是x的取值范围(区间表示).
考点:函数单调性的判断与证明,函数解析式的求解及常用方法
专题:函数的性质及应用
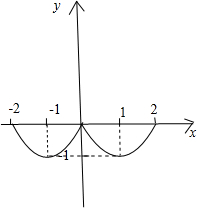
分析:(1)f(x)在[0,2]上的图象为抛物线,根据图象可求出f(x)在[0,2]上的解析式,根据偶函数根据y轴对称,可画出f(x)在[-2,0)上的图象,从而求出f(x)在[-2,0)上的解析式,这样就可求出函数f(x)在[-2,2]上的解析式;
(2)根据图象即可找出函数f(x)的单调区间及最小值;
(3根据图象可求得x的取值范围.
(2)根据图象即可找出函数f(x)的单调区间及最小值;
(3根据图象可求得x的取值范围.
解答:
 解:(1)根据已知条件得:y=f(x)=
解:(1)根据已知条件得:y=f(x)=
;
(2)根据偶函数图象关于y轴的对称性,画出y=f(x)在[-2,0)上的图象为:
根据图象可得到函数f(x)在[-2,2]上的单调增区间为[-1,0],[1,2],单调减区间为[-2,-1),(0,1);最小值为-1;
(3)通过图象看出f(x)<0的解为(-2,0)∪(0,2).
 解:(1)根据已知条件得:y=f(x)=
解:(1)根据已知条件得:y=f(x)=
|
(2)根据偶函数图象关于y轴的对称性,画出y=f(x)在[-2,0)上的图象为:
根据图象可得到函数f(x)在[-2,2]上的单调增区间为[-1,0],[1,2],单调减区间为[-2,-1),(0,1);最小值为-1;
(3)通过图象看出f(x)<0的解为(-2,0)∪(0,2).
点评:考查根据二次函数图象求函数解析式,偶函数的概念及图象的对称性,由图象找单调区间的方法.

练习册系列答案
相关题目
 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2,点M是线段PD的中点.点N在线段PD上,且
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2,点M是线段PD的中点.点N在线段PD上,且