题目内容
12.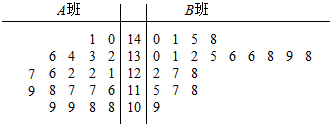 为备战“全国高中数学联赛”,我市某高中拟成立两个“数学竞赛班”,经过学校预选,选出40名学生,编成A,B两个班,分别由两位教师担任教练进行培训;经过两个月的培训,参加了市里组织的数学竞赛初赛(只有经过初赛,取得相应名次,才能取得参加省统一组织的“全国高中数学联赛”复赛资格),这40名学生的初赛成绩的茎叶图如图:
为备战“全国高中数学联赛”,我市某高中拟成立两个“数学竞赛班”,经过学校预选,选出40名学生,编成A,B两个班,分别由两位教师担任教练进行培训;经过两个月的培训,参加了市里组织的数学竞赛初赛(只有经过初赛,取得相应名次,才能取得参加省统一组织的“全国高中数学联赛”复赛资格),这40名学生的初赛成绩的茎叶图如图:市数学会规定:140分以上(含140分)为市级一等奖,135分以上(含135分)为市级二等奖,100分以上(含100分)为市级三等奖.
(1)由茎叶图判断A班和B班的平均分$\overline{{x}_{A}}$,$\overline{{x}_{B}}$的大小(只需写出结论);
(2)按照规则:获得市一等奖、二等奖的同学才能获得省里组织的“全国数学联赛”复赛资格,我们称这些同学为“种子选手”,请填写下面的2×2列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为称为“种子选手”与班级有关?
| A班 | B班 | 合计 | |
| 种子选手 | |||
| 非种子选手 | |||
| 合计 |
下面临界值表仅供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)根据茎叶图可知A班数据的重心偏下,可得:故$\overline{{x}_{A}}$<$\overline{{x}_{B}}$;
(2)根据茎叶图求出列联表中各个数据,计算出临界值,可得结论;
(3)由(2)知:种子选手共13人,其中获市一等奖的人数为6人,由题意,X满足参数为13,6,3的超几何分布所以X的所有可能取值为0,1,2,3,求出相应的概率,可得答案.
解答 解:(1)茎叶图可知A班数据的重心偏下,故$\overline{{x}_{A}}$<$\overline{{x}_{B}}$;
(2)由茎叶图可知,“种子选手”共有13名,其中A班3人,B班10人,非种子选手27人,其中A班17人,B班10人,从而2×2联表如下:
| A班 | B班 | 合计 | |
| 种子选手 | 3 | 10 | 13 |
| 非种子选手 | 17 | 10 | 27 |
| 合计 | 20 | 20 | 40 |
K2=$\frac{40×(3×10-17×10)^{2}}{20×20×27×13}$≈5.584
因为5.584>5.024,所以能够“在犯错误的概率不超过0.025的前提下”认为成为‘种子选手’与班级有关…(8分)
(3)由(2)知:种子选手共13人,其中获市一等奖的人数为6人,由题意,X满足参数为13,6,3的超几何分布所以X的所有可能取值为0,1,2,3,
∴P(X=0)=$\frac{{C}_{6}^{0}{C}_{7}^{3}}{{C}_{13}^{3}}$=$\frac{35}{286}$,P(X=1)=$\frac{{C}_{6}^{1}{C}_{7}^{2}}{{C}_{13}^{3}}$=$\frac{126}{286}$=$\frac{63}{143}$,
P(X=2)=$\frac{{C}_{6}^{2}{C}_{7}^{1}}{{C}_{13}^{3}}$=$\frac{105}{286}$,P(X=3)=$\frac{{C}_{6}^{3}{C}_{7}^{0}}{{C}_{13}^{3}}$=$\frac{20}{286}$=$\frac{10}{143}$…(10分)
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{35}{286}$ | $\frac{63}{143}$ | $\frac{105}{286}$ | $\frac{10}{143}$ |
(或由超几何分布的期望计算公式EX=n×$\frac{M}{N}$=3×$\frac{6}{13}$=$\frac{18}{13}$)
点评 本题考查的知识点是独立性检验,茎叶图,古典概型,是统计和概率的综合应用,难度中档.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.某小型贸易公司为了实现年终10万元利润目标,特制定了一个销售人员年终绩效奖励方案,当销售利润为x万元(4≤x≤10)时,奖金y万元随销售利润x的增加而增加,但奖金总数不超过2万元,同时奖金不超过销售利润的$\frac{1}{2}$,则下列函数中,符合该公司奖励方案的函数模型是(参考数据:lg2≈0.3,lg3≈0.48,lg5≈0.7)( )
| A. | y=0.4x | B. | y=lgx+1 | C. | y=x${\;}^{\frac{3}{2}}$ | D. | y=1.125x |
4.以(-2,1)为圆心且与直线x+y=3相切的圆的方程为( )
| A. | (x-2)2+(y+1)2=2 | B. | (x+2)2+(y-1)2=4 | C. | (x-2)2+(y+1)2=8 | D. | (x+2)2+(y-1)2=8 |
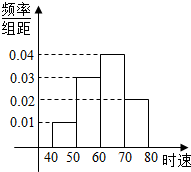 5000辆汽车通过某一段公路时的时速频率分布直方图如图所示.问:
5000辆汽车通过某一段公路时的时速频率分布直方图如图所示.问: