题目内容
已知双曲线x2-
=1.
(1)求以点A(2,1)为中点的弦所在直线方程;
(2)过点A(2,1)的直线L与所给的双曲线交于两点P1及P2,求线段P1P2的中点P的轨迹方程.
(3)过点B(1,1)能否作直线m,使m与所给双曲线交于两点Q1及Q2,且点B是线段Q1Q2的中点?这样的直线m如果存在,求出它的方程;如果不存在,说明理由.
| y2 |
| 2 |
(1)求以点A(2,1)为中点的弦所在直线方程;
(2)过点A(2,1)的直线L与所给的双曲线交于两点P1及P2,求线段P1P2的中点P的轨迹方程.
(3)过点B(1,1)能否作直线m,使m与所给双曲线交于两点Q1及Q2,且点B是线段Q1Q2的中点?这样的直线m如果存在,求出它的方程;如果不存在,说明理由.
考点:直线与圆锥曲线的关系,双曲线的简单性质
专题:直线与圆,圆锥曲线的定义、性质与方程
分析:(1)设A(2,1)是弦P1P2的中点,且P1(x1,y1),P2(x2,y2),利用点差法能求出以A(2,1)为中点的双曲线的弦所在的直线方程.
(2)设A(x1,y1),B(x2,y2),P(x,y),则2x12-y12=2,2x22-y22=2,两式相减,利用P是中点及斜率相等可求P得轨迹方程,从而得到其轨迹.
(3)假设直线l存在.由已知条件利用点差法求出直线l的方程为2x-y-1=0,联立方程组
,得2x2-4x+3=0,由△-8<0,推导出直线l不存在.
(2)设A(x1,y1),B(x2,y2),P(x,y),则2x12-y12=2,2x22-y22=2,两式相减,利用P是中点及斜率相等可求P得轨迹方程,从而得到其轨迹.
(3)假设直线l存在.由已知条件利用点差法求出直线l的方程为2x-y-1=0,联立方程组
|
解答:
解:(1)双曲线x2-
=1方程可化为:2x2-y2=2,
设A(2,1)是弦P1P2的中点,
且P1(x1,y1),P2(x2,y2),则x1+x2=4,y1+y2=2.
∵P1,P2在双曲线上,
∴
,
∴2(x1+x2)(x1-x2)-(y1-y2)(y1+y2)=0,
∴2×4(x1-x2)=2(y1-y2),
∴k=
=4,
∴以A(2,1)为中点的双曲线的弦所在的直线方程为:
y-1=4(x-2),整理得4x-y-7=0.
(2)设P1(x1,y1),P2(x2,y2),P(x,y),则x1+x2=2x,y1+y2=2y,
∵2x12-y12=2,2x22-y22=2,
∴4x(x1-x2)-2y(y1-y2)=0,
∴直线P1P2的斜率k=
=
,
∵kAP=
,A,P,P1P2共线,
∴
=
,
∴2x2-y2-4x+y=0,
即线段P1P2的中点P的轨迹方程是2x2-y2-4x+y=0.
(3)假设直线l存在.
设B(1,1)是弦MN的中点,
且Q1(x1,y1),Q2(x2,y2),则x1+x2=2,y1+y2=2.
∵Q1,Q2在双曲线上,
∴
,
∴2(x1+x2)(x1-x2)-(y1-y2)(y1+y2)=0,
∴4(x1-x2)=2(y1-y2),
∴k=
=2,
∴直线l的方程为y-1=2(x-1),即2x-y-1=0,
联立方程组
,得2x2-4x+3=0
∵△=16-4×3×2=-8<0,
∴直线l与双曲线无交点,
∴直线l不存在.
| y2 |
| 2 |
设A(2,1)是弦P1P2的中点,
且P1(x1,y1),P2(x2,y2),则x1+x2=4,y1+y2=2.
∵P1,P2在双曲线上,
∴
|
∴2(x1+x2)(x1-x2)-(y1-y2)(y1+y2)=0,
∴2×4(x1-x2)=2(y1-y2),
∴k=
| y1-y2 |
| x1-x2 |
∴以A(2,1)为中点的双曲线的弦所在的直线方程为:
y-1=4(x-2),整理得4x-y-7=0.
(2)设P1(x1,y1),P2(x2,y2),P(x,y),则x1+x2=2x,y1+y2=2y,
∵2x12-y12=2,2x22-y22=2,
∴4x(x1-x2)-2y(y1-y2)=0,
∴直线P1P2的斜率k=
| y1-y2 |
| x1-x2 |
| 2x |
| y |
∵kAP=
| y-1 |
| x-2 |
∴
| y-1 |
| x-2 |
| 2x |
| y |
∴2x2-y2-4x+y=0,
即线段P1P2的中点P的轨迹方程是2x2-y2-4x+y=0.
(3)假设直线l存在.
设B(1,1)是弦MN的中点,
且Q1(x1,y1),Q2(x2,y2),则x1+x2=2,y1+y2=2.
∵Q1,Q2在双曲线上,
∴
|
∴2(x1+x2)(x1-x2)-(y1-y2)(y1+y2)=0,
∴4(x1-x2)=2(y1-y2),
∴k=
| y1-y2 |
| x1-x2 |
∴直线l的方程为y-1=2(x-1),即2x-y-1=0,
联立方程组
|
∵△=16-4×3×2=-8<0,
∴直线l与双曲线无交点,
∴直线l不存在.
点评:本题考查直线方程的求法,是中档题,解题时要认真审题,注意点差法和根的判别式的合理运用.

练习册系列答案
相关题目
设集合A={-1,0,1},B={x|x2-x<2},则集合A∩B=( )
| A、{-1,0,1} |
| B、{-1,0} |
| C、{0,1} |
| D、{-1,1} |
三次函数f(x)=x3+bx2+cx+d(b,c,d∈R)在区间[-1,2]上是减函数,那么b+c的取值范围是( )
A、(-∞,
| ||
B、(-∞, -
| ||
| C、A(x0,f(x0)) | ||
D、(-∞,-
|
已知F1,F2为双曲线C:
-y2=1的左、右焦点,点P在C上,|PF1|=2|PF2|,则cos∠F1PF2=( )
| x | 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知A,B是两个相互独立事件,P(A),P(B)分别表示它们发生的概率,则1-P(A)P(B)是下列哪个事件的概率( )
| A、事件A,B同时发生 |
| B、事件A,B至少有一个发生 |
| C、事件A,B至多有一个发生 |
| D、事件A,B都不发生 |
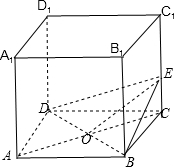 如图,正方体ABCD-A1B1C1D1,边长为1,E为CC1上一点,且EC=
如图,正方体ABCD-A1B1C1D1,边长为1,E为CC1上一点,且EC=