题目内容
12. 已知四棱锥P-ABCD,底面ABCD是∠A=60°的菱形,又PD⊥底面ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.
已知四棱锥P-ABCD,底面ABCD是∠A=60°的菱形,又PD⊥底面ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.(Ⅰ)证明:DN∥平面PMB;
(Ⅱ)求二面角P-AB-D的余弦值.
分析 (1)取BC中点G,连接DG、NG,由N为PC中点,可得NG∥PB,进一步得到NG∥平面PMB,再由已知可得四边形BGDM为平行四边形,得DG∥MB,则DG∥平面PMB,由面面平行的判定可得平面DNG∥平面PMB,则DN∥平面PMB;
(2)由底面ABCD为平行四边形,且∠A=60°,得△ABD为正三角形,取AB中点H,连接DH,PH,结合PD⊥底面ABCD,可得∠PHD为二面角P-AB-D的平面角,然后求解直角三角形可得二面角P-AB-D的余弦值.
解答 (1)证明:如图,
取BC中点G,连接DG、NG,∵N为PC中点,∴NG∥PB,则NG∥平面PMB,
∵AD∥BC,M为AD的中点,G为BC的中点,
∴MD∥BG,MD=BG,∴四边形BGDM为平行四边形,则DG∥MB,则DG∥平面PMB,
又NG∩DG=G,∴平面DNG∥平面PMB.
则DN∥平面PMB;
(2)解:∵底面ABCD为平行四边形,且∠A=60°,则△ABD为正三角形,
取AB中点H,连接DH,PH,∴DH⊥AB,
∵PD⊥底面ABCD,∴PD⊥AB,则AB⊥平面PDH,∴∠PHD为二面角P-AB-D的平面角.
设PD=CD=a,则DH=$\frac{\sqrt{3}a}{2}$,∴PH=$\sqrt{{a}^{2}+(\frac{\sqrt{3}}{2}a)^{2}}=\frac{\sqrt{7}}{2}a$,
则cos∠PHD=$\frac{DH}{PH}=\frac{\frac{\sqrt{3}}{2}a}{\frac{\sqrt{7}}{2}a}=\frac{\sqrt{21}}{7}$.
∴二面角P-AB-D的余弦值为$\frac{{\sqrt{21}}}{7}$.
点评 本题考查直线与平面平行的判定,考查了二面角的平面角的求法,正确找出二面角的平面角是解答该题的关键,是中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $(\frac{π}{3},\frac{{\sqrt{3}}}{2}-\frac{π}{6})$ | B. | $(-\frac{π}{3},\frac{π}{6}-\frac{{\sqrt{3}}}{2})$ | C. | $x=\frac{π}{3}$ | D. | $x=-\frac{π}{3}$ |
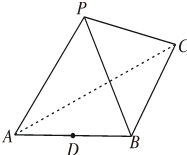 在三棱锥P-ABC中,△PBC和△PAC是边长为$\sqrt{2}$的等边三角形,AB=2,D是AB中点.
在三棱锥P-ABC中,△PBC和△PAC是边长为$\sqrt{2}$的等边三角形,AB=2,D是AB中点. 如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的一点,且BF⊥平面ACE,AC与BD交于点G.
如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的一点,且BF⊥平面ACE,AC与BD交于点G.