题目内容
15.△ABC的外接圆圆心为O,半径为2,$\overrightarrow{OA}+\overrightarrow{AB}+\overrightarrow{AC}$=$\overrightarrow 0$,且$|{\overrightarrow{OA}}|=|{\overrightarrow{AB}}$|,则$\overrightarrow{CB}$在$\overrightarrow{CA}$方向上的投影为( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 3 |
分析 根据$\overrightarrow{OA}+\overrightarrow{AB}+\overrightarrow{AC}$=$\overrightarrow 0$得出$\overrightarrow{OB}$=$\overrightarrow{CA}$,判断四边形OBAC是平行四边形,
结合$|{\overrightarrow{OA}}|=|{\overrightarrow{AB}}$|得到四边形OBAC是边长为2的菱形且∠ABO=∠AC0=60°,
再利用向量投影的定义即可算出答案.
解答 解:∵$\overrightarrow{OA}+\overrightarrow{AB}+\overrightarrow{AC}$=$\overrightarrow 0$,
∴$\overrightarrow{OA}$+$\overrightarrow{AB}$=-$\overrightarrow{AC}$,
即$\overrightarrow{OB}$=$\overrightarrow{CA}$,
∴四边形OBAC是平行四边形,如图所示;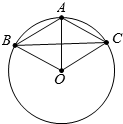
又∵△ABC的外接圆的圆心为O,半径为2,
∴|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|=2,
又$|{\overrightarrow{OA}}|=|{\overrightarrow{AB}}$|,
∴四边形OBAC是边长为2的菱形,且∠ABO=∠ACO=60°,
∴∠ACB=$\frac{1}{2}$∠ACO=30°,
|$\overrightarrow{CB}$|=$\sqrt{{2}^{2}{+2}^{2}-2×2×2×cos120°}$=2$\sqrt{3}$;
∴向量$\overrightarrow{CB}$在$\overrightarrow{CA}$方向上的投影为:
|$\overrightarrow{CB}$|cos30°=2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=3.
故选:D.
点评 本题考查了三角形外接圆的向量表示以及求向量的投影问题,着重考查了向量的加法法则、向量数量积的运算性质和向量在几何中的应用问题,是综合性题目.

| A. | 2n-1 | B. | 2n | C. | 2n+1 | D. | 2n+2 |
| A. | 梯形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
 如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的一点,且BF⊥平面ACE,AC与BD交于点G.
如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的一点,且BF⊥平面ACE,AC与BD交于点G.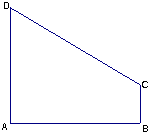 如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,AB=2,AD=$\frac{3}{2}$,BC=$\frac{1}{2}$,椭圆以A、B为焦点且经过点D.
如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,AB=2,AD=$\frac{3}{2}$,BC=$\frac{1}{2}$,椭圆以A、B为焦点且经过点D.