题目内容
如图,已知椭圆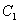 与
与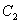 的中心在坐标原点
的中心在坐标原点 ,长轴均为
,长轴均为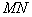 且在
且在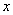 轴上,短轴长分别为
轴上,短轴长分别为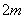 ,
,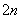
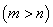 ,过原点且不与
,过原点且不与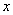 轴重合的直线
轴重合的直线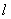 与
与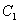 ,
,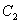 的四个交点按纵坐标从大到小依次为
的四个交点按纵坐标从大到小依次为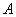 ,
,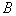 ,
, ,
,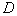 。记
。记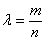 ,
,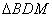 和
和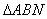 的面积分别为
的面积分别为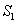 和
和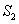 。
。
(I)当直线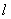 与
与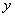 轴重合时,若
轴重合时,若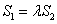 ,求
,求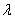 的值;
的值;
(II)当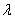 变化时,是否存在与坐标轴不重合的直线
变化时,是否存在与坐标轴不重合的直线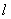 ,使得
,使得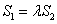 ?并说明理由。
?并说明理由。
【解析】(Ⅰ)依题意可设椭圆 和
和 的方程分别为
的方程分别为
 :
: ,
, :
: . 其中
. 其中 ,
,
解法1:如图1,若直线 与
与 轴重合,即直线
轴重合,即直线 的方程为
的方程为 ,则
,则
 ,
, ,所以
,所以 .
.
在C1和C2的方程中分别令 ,可得
,可得 ,
, ,
, ,
,
于是 .
.
若 ,则
,则 ,化简得
,化简得 . 由
. 由 ,可解得
,可解得 .
.
故当直线 与
与 轴重合时,若
轴重合时,若 ,则
,则 .
.
解法2:如图1,若直线 与
与 轴重合,则
轴重合,则
 ,
, ;
;
 ,
, .
.


所以 .
.
若 ,则
,则 ,化简得
,化简得 . 由
. 由 ,可解得
,可解得 .
.
故当直线 与
与 轴重合时,若
轴重合时,若 ,则
,则 .
.
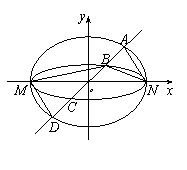
(Ⅱ)解法1:如图2,若存在与坐标轴不重合的直线l,使得 . 根据对称性,
. 根据对称性,
不妨设直线 :
: ,
,
点 ,
, 到直线
到直线 的距离分别为
的距离分别为 ,
, ,则
,则
因为 ,
, ,所以
,所以 .
.
又 ,
, ,所以
,所以 ,即
,即 .
.
由对称性可知 ,所以
,所以 ,
,
 ,于是
,于是
 . ①
. ①
将 的方程分别与C1,C2的方程联立,可求得
的方程分别与C1,C2的方程联立,可求得
 ,
, .
.
根据对称性可知 ,
, ,于是
,于是
 . ②
. ②
从而由①和②式可得
 . ③
. ③
令 ,则由
,则由 ,可得
,可得 ,于是由③可解得
,于是由③可解得 .
.
因为 ,所以
,所以 . 于是③式关于
. 于是③式关于 有解,当且仅当
有解,当且仅当 ,
,
等价于 . 由
. 由 ,可解得
,可解得 ,
,
即 ,由
,由 ,解得
,解得 ,所以
,所以
当 时,不存在与坐标轴不重合的直线l,使得
时,不存在与坐标轴不重合的直线l,使得 ;
;
当 时,存在与坐标轴不重合的直线l使得
时,存在与坐标轴不重合的直线l使得 .
.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
 ,用Ⅱn
,用Ⅱn 表示它的前n项之积:Ⅱn=a1·a2…an,则Ⅱ1,Ⅱ2…中最大的是 ( )
表示它的前n项之积:Ⅱn=a1·a2…an,则Ⅱ1,Ⅱ2…中最大的是 ( ) 恒成立,则实数a的取值范围是 .
恒成立,则实数a的取值范围是 . 的焦点为
的焦点为 、
、 ,点
,点 在双曲线上且
在双曲线上且 轴,则
轴,则 的距离为 。
的距离为 。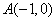 ,
,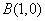 ,
,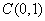 ,直线
,直线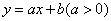 将
将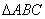 分割为面积相等的两部分,则
分割为面积相等的两部分,则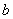 的取值范围是( )
的取值范围是( ) (B)
(B)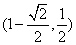 (C)
(C)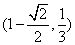 (D)
(D)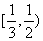
 ,则
,则 化简后的最后结果等于______________。
化简后的最后结果等于______________。 平面上有一系列的点
平面上有一系列的点 ,对于所有正整
,对于所有正整 ,点
,点 位于函数
位于函数 的图像上,以点
的图像上,以点 轴相切,且圆
轴相切,且圆 又彼此外切,且
又彼此外切,且 。则
。则 等于 。
等于 。 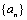 是首项大于零的等比数列,则“
是首项大于零的等比数列,则“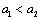 ”是“数列
”是“数列 B.8+
B.8+ C.8+
C.8+ D.8+
D.8+
