题目内容
设数列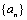
是首项大于零的等比数列，则“
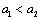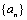”是“数列是递增数列”的( )
A．充分而不必要条件 B．必要而不充分条件
C．充分必要条件 D．既不充分也不必要条件
C
练习册系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
双基同步导航训练系列答案黄冈小状元同步计算天天练系列答案题目内容
设数列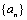是首项大于零的等比数列，则“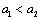”是“数列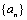是递增数列”的( )
A．充分而不必要条件 B．必要而不充分条件
C．充分必要条件 D．既不充分也不必要条件
C
双基同步导航训练系列答案黄冈小状元同步计算天天练系列答案
，其中
为实常数。
的单调性；
在
上恒成立，求实数
，设
，
。是否存在实常数
，既使
又使
对一切
恒成立？若存在，试找出
与
的中心在坐标原点
，长轴均为
且在
轴上，短轴长分别为
，
，过原点且不与
与
，
，
，
。记
，
和
的面积分别为
和
。
轴重合时，若
，求
的值；
中，已知
，
，且
的值。
的值为 ( )
（其中
）成立的
的取值范围是 ．
，
，已知函数
在
上的最大值为6．
的值；
，
．求
的值．
，b=
，设函数
=a
b．
的单调递增区间；
个单位，得到函数
的图象，求函数
上的最大值和最小值．
的点
构成的平面区域的面积为
，满足条件
的点
（其中
，
分别表示不大于x，y的最大整数，例如
，
），给出下列结论：
在直线
左上方的区域内；
左下方的区域内；
；
．