题目内容
在△ABC中，已知a=2
，b=6，A=30°，B为锐角，求B及S△ABC．
| 3 |
考点：正弦定理
专题：解三角形
分析：由条件利用正弦定理求得sinB的值，可得B的值，利用三角形内角和公式求得C=90°，从而求得 S△ABC =
ab的值．
| 1 |
| 2 |
解答：
解：△ABC中，∵已知a=2
，b=6，A=30°，B为锐角，∴由正弦定理可得
=
，
即
=
，解得sinB=
，B=60°，∴C=180°-A-B=90°．
∴S△ABC =
ab=6
．
| 3 |
| a |
| sinA |
| b |
| sinB |
即
2
| ||
| sin30° |
| 6 |
| sinB |
| ||
| 2 |
∴S△ABC =
| 1 |
| 2 |
| 3 |
点评：本题主要考查正弦定理的应用，根据三角函数的值求角，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
已知f（x）=x3+3x2-mx+1在[-2，2]上为单调增函数，则实数m的取值范围为（ ）
| A、m≤-3 | B、m≤0 |
| C、m≥-24 | D、m≥-1 |
为了帮助小型企业乙转型发展，大型国企甲将经营状况良好的某种消费品专卖批发店，以120万元的优惠价格转让给了企业乙，并约定从该店经营的利润中，首先保证所有职工每月工资开支10万元，再逐步偿还转让费（不计息），在国企甲提供的资料中显示：①这种消费品的进价为每件20元；②该店月销量Q（千件）与销售价格x（元）的关系如图所示；③每月需水电房租等各种开支22000元．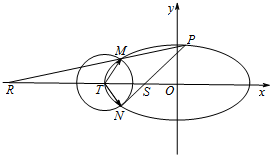
如图，已知椭圆C：