Question

已知函数f（x）=x+

1

x

．
（1）判断函数f（x）的奇偶性，并画出函数f（x）的简图；
（2）求出函数f（x）的单调区间；
（3）求函数g（x）=x+

1

x+1

（x≥2）的最小值．

Answer 1

考点：函数奇偶性的判断,函数的单调性及单调区间,函数的最值及其几何意义

专题：函数的性质及应用

分析：（1）根据函数奇偶性的定义即可判断f（x）为奇函数，然后通过x取几个值，并求出对应的f（x）值，通过描点、连线画出f（x）在（0，+∞）的简图，再根据f（x）图象根据原点对称，画出它在（-∞，0）的图象；
（2）通过函数f（x）图象即可得到f（x）的单调区间；
（3）令y=g（x），x+1=t，t≥3，原函数变成y=t+

1

t

-1，根据（2）判断函数t+

1

t

在[3，+∞）的单调性，根据单调性即可求出该函数的最小值，从而求出t+

1

t

-1的最小值，即求出g（x）的最小值．

解答： 解：（1）函数f（x）的定义域为{x|x≠0}，f（-x）=-x-

1

x

=-（x+

1

x

）=-f（x）；
∴函数f（x）是奇函数，则f（x）的图象关于原点对称；
x=

1

2

，1，2，3，4时，对应的f（x）=

5

2

，2，

5

2

，

10

3

，

17

4

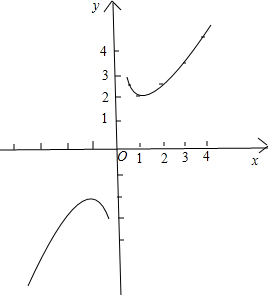
，通过描点连线即可画出f（x）在（0，+∞）上的图象，并根据f（x）图象关于原点对称，作出f（x）在（-∞，0）的图象，如下图所示：
（2）由图象可看出f（x）的单调增区间为：（-∞，-1），（1，+∞），单调减区间为：（0，1]，[-1，0）；
（3）令y=g（x），x+1=t，t≥3，则：
y=t+

1

t

-1，由（2）知t+

1

t

在[3，+∞）上单调递增，所以t=3时，t+

1

t

取最小值

10

3

；
∴t+

1

t

-1取最小值

7

3

；
∴g（x）的最小值为

7

3

．

点评：考查奇函数的定义，画函数简图的方法，根据图象找函数的单调区间，以及根据函数单调性求函数的最值．