题目内容
1.已知偶函数f(x)的定义域为R,若f(x-1)为奇函数,且f(2)=3,则f(5)+f(6)的值为( )| A. | -3 | B. | -2 | C. | 2 | D. | 3 |
分析 根据函数的奇偶性的性质,得到f(x+4)=f(x),即可得到结论.
解答 解:∵f(x-1)为奇函数,
∴f(-x-1)=-f(x-1),
∵f(x)是偶函数,
∴f(-x-1)=f(x+1)=-f(x-1),
即f(x+2)=-f(x),
f(x+4)=f(x+2+2)=-f(x+2)=f(x),
则f(5)=f(1),
f(6)=f(2)=3,
当x=-1时,由f(x+2)=-f(x),
得f(1)=-f(-1)=-f(1),
即f(1)=0,
∴f(5)+f(6)=3,
故选:D.
点评 本题主要考查函数值的计算,利用函数奇偶性的性质,得到函数的对称轴是解决本题的关键.

练习册系列答案
相关题目
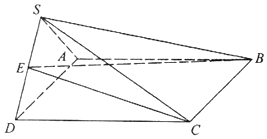 如图,四棱锥S-ABCD中,底面ABCD是边长为4的正方形,平面SAD⊥平面SCD,$SA=SD=2\sqrt{2}$.
如图,四棱锥S-ABCD中,底面ABCD是边长为4的正方形,平面SAD⊥平面SCD,$SA=SD=2\sqrt{2}$.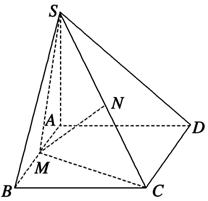 如图所示,在四棱锥S-ABCD中,AD∥BC,AD⊥AB,CD⊥平面SAD,SA=AD=2,AB=1,SB=$\sqrt{5}$,SD=2$\sqrt{2}$,M,N分别为AB,SC的中点.
如图所示,在四棱锥S-ABCD中,AD∥BC,AD⊥AB,CD⊥平面SAD,SA=AD=2,AB=1,SB=$\sqrt{5}$,SD=2$\sqrt{2}$,M,N分别为AB,SC的中点.