题目内容
已知向量
=(1+sin2x,sinx-cosx),
=(1,sinx+cosx),函数f(x)=
•
.
(Ⅰ)求f(x)的最大值及相应的x的值;
(Ⅱ)在△ABC中,a,b,c分别是三个内角A,B,C所对边,若f(
)=2,a=2,求△ABC面积的最大值.
| a |
| b |
| a |
| b |
(Ⅰ)求f(x)的最大值及相应的x的值;
(Ⅱ)在△ABC中,a,b,c分别是三个内角A,B,C所对边,若f(
| A |
| 2 |
考点:基本不等式在最值问题中的应用,三角函数中的恒等变换应用
专题:解三角形,不等式的解法及应用
分析:(Ⅰ)化为y=1+
sin(2x-
),根据函数图象求解.(Ⅱ)知f(
)=2时,sin(A-
)=
,即A=
+2kπ或A=π+2kπ,k∈Z,求解即可.
| 2 |
| π |
| 4 |
| A |
| 2 |
| π |
| 4 |
| ||
| 2 |
| π |
| 2 |
解答:
解:(Ⅰ)∵
=(1+sin2x,sinx-cosx),
=(1,sinx+cosx),
∴f(x)=
•
=1+sin2x+sin2x-cos2x,
=1+sin2x-cos2x,
=1+
sin(2x-
),
∴当2x-
=2kπ+
即x=
+kπ,k∈Z时,
函数取得最大值1+
.
(Ⅱ)由(I)知f(
)=2时,sin(A-
)=
,
∴A-
=2kπ+
或A-
=2kπ+
,
即A=
+2kπ或A=π+2kπ,k∈Z,
∵A是三角形的一个内角,
∴A=
,即△ABC是直角三角形.
∵a=2,∴b2+c2=4,
∴S△ABC=
bc≤
=1(当且仅当b=c=
时,取得最大值),
∴△ABC面积的最大值为1.
| a |
| b |
∴f(x)=
| a |
| b |
=1+sin2x-cos2x,
=1+
| 2 |
| π |
| 4 |
∴当2x-
| π |
| 4 |
| π |
| 2 |
| 3π |
| 8 |
函数取得最大值1+
| 2 |
(Ⅱ)由(I)知f(
| A |
| 2 |
| π |
| 4 |
| ||
| 2 |
∴A-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
即A=
| π |
| 2 |
∵A是三角形的一个内角,
∴A=
| π |
| 2 |
∵a=2,∴b2+c2=4,
∴S△ABC=
| 1 |
| 2 |
| b2+c2 |
| 4 |
| 2 |
∴△ABC面积的最大值为1.
点评:本题考查了三角函数的性质,均值不等式的求解,属于难题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
若原点和点(1,1)都在直线x+y=a的同一侧,则a的取值范围是( )
| A、a<0或a>2 |
| B、0<a<2 |
| C、a=0或a=2 |
| D、0≤a≤2 |
如图给出的是计算
+
+
+…+
的值的一个程序框图,其中判断框中应填入的是( )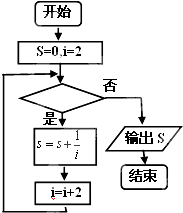
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 100 |

| A、i>100 | B、i≤100 |
| C、i>50 | D、i≤50 |
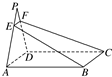 如图所示,四边形ABCD是矩形,P∉平面ABCD,过BC作平面BCFE交AP于E,交DP于F.
如图所示,四边形ABCD是矩形,P∉平面ABCD,过BC作平面BCFE交AP于E,交DP于F.

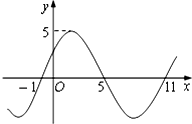 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0≤φ<2π)在R上的部分图象如图所示,则f(2014)=
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0≤φ<2π)在R上的部分图象如图所示,则f(2014)=