题目内容
15.在△ABC中,角A,B,C的对边分别为,且满足$\frac{2c-b}{a}=\frac{cosB}{cosA}$.(1)求角A的大小;
(2)若D为BC上一点,且$\overrightarrow{CD}=2\overrightarrow{DB},b=3,|{AD}|=\sqrt{21}$,求a.
分析 (1)由题意根据正弦定理求得∴(2sinC-sinB)cosA=sinAcosB,由A=π-(B+C),根据诱导公式及两角和正弦公式,即可求得A的值;
(2)过D作DE∥AB于E,则△ADE中,ED=$\frac{1}{3}$AC=1,∠DEA=$\frac{2π}{3}$,由余弦定理可知△ABC为直角三角形,a=BC=3$\sqrt{3}$.
解答  解:(1)由$\frac{2c-b}{a}=\frac{cosB}{cosA}$,则(2c-b)cosA=acosB,
解:(1)由$\frac{2c-b}{a}=\frac{cosB}{cosA}$,则(2c-b)cosA=acosB,
由正弦定理可知:$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R,则a=2RsinA,b=2RsinB,c=2RsinC,
∴(2sinC-sinB)cosA=sinAcosB,
整理得:2sinCcosA-sinBcosA=sinAcosB,
由A=π-(B+C),则sinA=sin[π-(B+C)]=sin(B+C),
即2sinCcosA=sin(A+B)=sinC,
由sinC≠0,则cosC=$\frac{1}{2}$,即A=$\frac{π}{3}$,
∴角A的大小$\frac{π}{3}$;
(2)过D作DE∥AB于E,则△ADE中,ED=$\frac{1}{3}$AC=1,∠DEA=$\frac{2π}{3}$,
由余弦定理可知AD2=AE2+ED2-2AE•EDcos$\frac{π}{3}$,
又AC=3,A=$\frac{π}{3}$,则△ABC为直角三角形,
∴a=BC=3$\sqrt{3}$,
∴a的值为3$\sqrt{3}$.
点评 本题考查正弦定理的即余弦定理的应用,考查两角和的正弦公式,考查计算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.执行如图程序框图,若输出y=4,则输入的x为( )


| A. | -3或-2或1 | B. | -2 | C. | -2或1 | D. | 1 |
20.执行如图所示的流程图,输出的S值为( )


| A. | $\frac{2}{3}$ | B. | $\frac{13}{21}$ | C. | $\frac{13}{7}$ | D. | $\frac{305}{357}$ |
7.若不等式|x+m|≤4的解集为A,且A⊆{x|-2≤x≤8},则实数m的取值范围是( )
| A. | [-4,-2] | B. | [-2,6] | C. | [0,8] | D. | [2,4] |
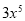 +
+ -8x+5在x=2时的值。
-8x+5在x=2时的值。