题目内容
7.若不等式|x+m|≤4的解集为A,且A⊆{x|-2≤x≤8},则实数m的取值范围是( )| A. | [-4,-2] | B. | [-2,6] | C. | [0,8] | D. | [2,4] |
分析 不等式|x+m|≤4,可得:-m-4≤x≤4-m,可得解集A,根据A⊆{x|-2≤x≤8},即可得出.
解答 解:不等式|x+m|≤4,可得:-m-4≤x≤4-m,解集A=[-m-4,4-m],
∵A⊆{x|-2≤x≤8},∴$\left\{\begin{array}{l}{-m-4≥-2}\\{4-m≤8}\end{array}\right.$,解得-4≤m≤-2.
则实数m的取值范围是[-4,-2].
故选:A.
点评 本题考查了不等式的性质与解法、集合的有关运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.下列说法错误的是( )
| A. | 空间中两条异面直线所成的角的范围是[0°,90°] | |
| B. | 平面直角坐标系中直线的倾斜角的范围是[0°,180°) | |
| C. | 二面角的平面角的范围是[0°,180°] | |
| D. | 直线与平面所成的角的范围是[0°,90°] |
2.若存在实数x,使|x-a|+|x-1|≤3成立,则实数a的取值范围是( )
| A. | [-2,1] | B. | [-2,2] | C. | [-2,3] | D. | [-2,4] |

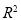 的值判断的拟合效果,
的值判断的拟合效果,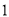 ;
;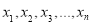 的方差为
的方差为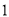 ,则
,则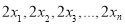 的方差为
的方差为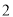 ;
;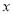 与
与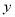 的随机变量
的随机变量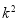 的观测值
的观测值 来说,
来说, 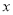 与
与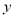 有关系”的把握程度越大.
有关系”的把握程度越大. B.
B. C.
C. D.
D.