题目内容

12．方程$（x+y-2）\sqrt{{x^2}+{y^2}-9}=0$表示的曲线是（　　）
A．一条直线和一个圆B．一条直线和半个圆
C．两条射线和一个圆D．一条线段和半个圆

分析 将方程等价变形，即可得出结论．

解答 解：由题意方程$（x+y-2）\sqrt{{x^2}+{y^2}-9}=0$可化为$\sqrt{{x}^{2}+{y}^{2}-9}$=0或x+y-2=0（x2+y2-9≥0）
∴方程$（x+y-2）\sqrt{{x^2}+{y^2}-9}=0$表示的曲线是两条射线和一个圆．
故选：C．

点评 本题考查轨迹方程，考查学生分析解决问题的能力，属于基础题．

练习册系列答案
相关题目
2．双曲线的中心在原点，离心率等于2，若它的一个顶点恰好是抛物线y2=8x的焦点，则双曲线的方程为$\frac{{x}^{2}}{1}-\frac{{y}^{2}}{3}=1$．
3．执行图中程序框图，如果输入x1=2，x2=3，x3=7，则输出的T值为（　　）
A．0B．4C．2D．3
20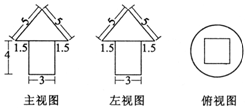．如图是一个几何体的三视图，尺寸如图所示，（单位：cm），则这个几何体的体积是（　　）
A．（10π+36）cm3B．（11π+35）cm3C．（12π+36）cm3D．（13π+34）cm3
7．已知函数f（x）=-3lnx+ax2+bx（a＞0，b∈R），若对任意x＞0都有f（x）≥f（3）成立，则（　　）
A．lna＞-b-1B．lna≥-b-1C．lna≤-b-1D．lna＜-b-1
17．某几何体的三视图如图所示，则俯视图的面积为（　　）
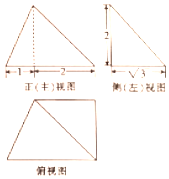
A．$5\sqrt{3}$B．$\frac{{5\sqrt{3}}}{2}$C．5D．$\frac{5}{2}$
4．若函数f（ x）=ax3-bx+c为奇函数，则c=（　　）
A．0B．1C．-1D．-2
1．设向量$\overrightarrow a，\overrightarrow b$的夹角为135°，且$|\overrightarrow a|=\sqrt{2}，|\overrightarrow b|=2$；
（1）求$\overrightarrow a•\overrightarrow b$的值；
（2）设$\overrightarrow c=x\overrightarrow a-\overrightarrow b（x∈R）$，当$|\overrightarrow c|$取得最小值时，求向量$\overrightarrow c$与$\overrightarrow b$夹角的大小．
2．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，且点（1，$\frac{3}{2}$）在椭圆E上．
（Ⅰ）求椭圆E的方程；
（Ⅱ）设动直线l：y=kx+m（k，m∈R）与椭圆E只有一个公共点P．
（1）用实数k，m表示点P的坐标；
（2）若动直线l与直线x=4相交于点Q，问：在x轴上是否存在定点M，使得MP⊥MQ？若存在，求出定点M的坐标；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网