题目内容
12.设f(x)的定义域为[-3,3],且f(x)是奇函数,当x∈[0,3]时,f(x)=x(1-3x).(1)求当x∈[-3,0)时,f(x)的解析式;
(2)解不等式f(x)<-8x.
分析 (1)根据函数奇偶性的性质进行求解即可.
(2)根据函数的解析式,利用分类讨论的思想解不等式即可.
解答 解:(1)若x∈[-3,0),则-x∈(0,3],
即f(-x)=-x(1-3-x).
∵f(x)是奇函数,
∴f(-x)=-x(1-3-x)=-f(x),
即f(x)=x(1-3-x).x∈[-3,0).
(2)若x∈[0,3]时,由f(x)=x(1-3x)<-8x.
得1-3x<-8,即3x>9,即2<x≤3,
若x∈[-3,0)时,由f(x)=x(1-3-x)<-8x.
得1-3-x>-8,即3-x<9,即-2<x<0,
综上不等式的解集为(-2,0)∪(2,3].
点评 本题主要考查函数解析式的求解以及不等式的求解,利用函数奇偶性的对称性以及指数函数的性质是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.在△ABC中,“A=$\frac{π}{4}$”是“cosA=$\frac{\sqrt{2}}{2}$“的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
20.函数$y=\frac{{\sqrt{4-{x^2}}}}{{1-{x^2}}}$的定义域为( )
| A. | [-2,2] | B. | [-2,-1)∪(-1,1)∪(1,2] | C. | (-∞,-2)∪(2,+∞) | D. | [-2,-1)∪(1,2] |
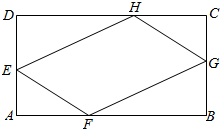 如图,在矩形ABCD中,已知AD=1.5,AB=a(a>1.5),E,F,G,H分别是边AD,AB,BC,CD上的动点,且满足AE=AF=CG=CH.若AE=x,当x变化时.
如图,在矩形ABCD中,已知AD=1.5,AB=a(a>1.5),E,F,G,H分别是边AD,AB,BC,CD上的动点,且满足AE=AF=CG=CH.若AE=x,当x变化时.