题目内容

4．数列$1，\frac{1}{2}，2，\frac{1}{4}，4，\frac{1}{8}$，…的前2n项和S2n=2n-$\frac{1}{{2}^{n}}$．

分析 由数列的求和方法：分组求和，结合等比数列的求和公式，计算即可得到所求和．

解答 解：S2n=（1+2+4+…+2n-1）+（$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{2n}$）
=$\frac{1-{2}^{n}}{1-2}$+$\frac{\frac{1}{2}（1-\frac{1}{{2}^{n}}）}{1-\frac{1}{2}}$
=2n-1+1-$\frac{1}{{2}^{n}}$=2n-$\frac{1}{{2}^{n}}$．
故答案为：2n-$\frac{1}{{2}^{n}}$．

点评 本题考查数列的求和方法：分组求和，注意运用等比数列的求和公式，考查运算能力，属于基础题．

练习册系列答案
相关题目
17．若$cos（\frac{π}{2}-α）=\frac{3}{5}$，则sin（π+α）的值为（　　）
A．$\frac{3}{5}$B．$-\frac{3}{5}$C．$\frac{4}{5}$D．$-\frac{4}{5}$
16．已知f（x）=Asin（x+$\frac{π}{4}$）（A≠0）．
（1）若A=1，将f（x）的图象上各点的纵坐标不变，横坐标扩大为原来的2倍，再将所得图象上各点的横坐标不变，纵坐标扩大为原来的2倍，得到g（x）的图象，求g（x）的解析式及对称轴方程．
（2）若α∈[0，π]，f（α）=cos2α，sin2α=-$\frac{7}{9}$，求A的值．
12．设f（x）的定义域为[-3，3]，且f（x）是奇函数，当x∈[0，3]时，f（x）=x（1-3x）．
（1）求当x∈[-3，0）时，f（x）的解析式；
（2）解不等式f（x）＜-8x．
19．已知一平面图形的斜二侧画法的水平放置的直观图如图所示，则原来图形的面积为（　　）
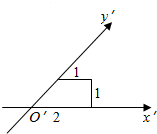
A．$\frac{3}{2}$B．3C．$3\sqrt{2}$D．$6\sqrt{2}$
9．设f（x）是定义在R上的偶函数，?x∈R，都有f（2-x）=f（2+x），且当x∈[0，2]时，f（x）=2x-2，若函数g（x）=f（x）-loga（x+1）（a＞0，a≠1）在区间（-1，9]内恰有三个不同零点，则实数a的取值范围是（$\frac{1}{9}$，$\frac{1}{5}$）∪（$\sqrt{3}$，$\sqrt{7}$）．
16．从1、2、3、4、5这五个数中任取三个数，则所取的三个数能构成等差数列的概率为（　　）
A．$\frac{1}{2}$B．$\frac{2}{5}$C．$\frac{3}{5}$D．$\frac{2}{3}$
13．设集合A={1，2}，则下列正确的是（　　）
A．1∈AB．1∉AC．{1}∈AD．1⊆A
12．已知函数f（x）=2sin2x+sin2x-1，x∈R．
（1）求f（x）的最小正周期；
（2）f（x）的最大值及取得最大值时x的集合；
（3）求f（x）的单调递减区间．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网