题目内容
已知A，B，C点在球O的球面上，∠BAC=90°，AB=AC=2．球心O到平面ABC的距离为1，则球O的表面积为（ ）
| A、12π | B、16π |
| C、36π | D、20π |
考点：球的体积和表面积
专题：计算题,空间位置关系与距离
分析：由∠BAC=90°，AB=AC=2，得到BC，即为A、B、C三点所在圆的直径，取BC的中点M，连接OM，则OM即为球心到平面ABC的距离，在Rt△OMB中，OM=1，MB=
，则OA可求．
| 2 |
解答：
解：如图所示：取BC的中点M，则球面上A、B、C三点所在的圆即为⊙M，连接OM，则OM即为球心到平面ABC的距离，
在Rt△OMB中，OM=1，MB=
，
∴OA=
，即球的半径为
，
∴球O的表面积为12π．
故选：A．
解：如图所示：取BC的中点M，则球面上A、B、C三点所在的圆即为⊙M，连接OM，则OM即为球心到平面ABC的距离，在Rt△OMB中，OM=1，MB=
| 2 |
∴OA=
| 3 |
| 3 |
∴球O的表面积为12π．
故选：A．
点评：本题考查球的有关计算问题，点到平面的距离，是基础题．
练习册系列答案
相关题目
设定义在R上的偶函数f（x）满足f（x+2）=f（x），当x∈[0，1]时，f（x）=x3，则方程f（x）=lg|x|根的个数为（ ）
| A、12 | B、16 | C、18 | D、20 |
如图，ABCD-A1B1C1D1为正方体，下面结论错误的是（ ）
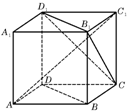
| A、BD∥平面CB1D1 |
| B、AC1⊥BD |
| C、AC1⊥平面CB1D1 |
| D、异面直线AC1与CB所成的角为60° |
已知命题p：x≥1，命题q：x2≥x，则p是q的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
函数y=xe-x，x∈[0，4]的最小值为（ ）
| A、0 | ||
B、
| ||
C、
| ||
D、
|