题目内容
17.设函数f(x)=$\sqrt{x-2}+\sqrt{11-x}$的最大值为M.(Ⅰ)求实数M的值;
(Ⅱ)求关于x的不等式|x-$\sqrt{2}$|+|x+2$\sqrt{2}$|≤M的解集.
分析 (Ⅰ)利用基本不等式以及重要不等式,转化求解函数的最值,即可求实数M的值;
(Ⅱ)通过绝对值不等式的几何意义,之间求关于x的不等式|x-$\sqrt{2}$|+|x+2$\sqrt{2}$|≤M的解集.
解答 (本小题满分10分)选修4-5:不等式选讲
解:(I)因为a,b>0时,$({\frac{a+b}{2})}^{2}≤\frac{{a}^{2}+{b}^{2}}{2}$,
所以$f(x)=\sqrt{x-2}+\sqrt{11-x}≤2\sqrt{\frac{(x-2)+(11-x)}{2}}=3\sqrt{2}$,
当且仅当$x=\frac{13}{2}$时等号成立. 故函数f(x)的最大值$M=3\sqrt{2}$---------------(5分)
(Ⅱ)由绝对值三角不等式可得$|{x-\sqrt{2}}|+|{x+2\sqrt{2}}|≥|{(x-\sqrt{2})-(x+2\sqrt{2})}|=3\sqrt{2}$.
所以不等式$|x-\sqrt{2}|+|x+2\sqrt{2}|≤3\sqrt{2}$的解x就是
方程$|x-\sqrt{2}|+|x+2\sqrt{2}|=3\sqrt{2}$的解.
由绝对值的几何意义得,当且仅当$-2\sqrt{2}≤x≤\sqrt{2}$时,$|x-\sqrt{2}|+|x+2\sqrt{2}|=3\sqrt{2}$.
所以不等式$|x-\sqrt{2}|+|x+2\sqrt{2}|≤M$的解集为:$\{x|-2\sqrt{2}≤x≤\sqrt{2}\}$--------------(10分)
点评 本题考查绝对值不等式的解法,绝对值不等式的几何意义,考查转化思想以及计算能力.

练习册系列答案
相关题目
5.海水受日月的引力,在一定的时候发生涨落的现象叫潮,一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是某港口在某季节每天的时间与水深关系表:
经长期观测,这个港口的水深与时间的关系,可近似用函数f(t)=Asin(ωt+ϕ)+b$(A,ω>0,|ϕ|<\frac{π}{2})$来描述.
(1)根据以上数据,求出函数f(t)=Asin(ωt+ϕ)+b的表达式;
(2)一条货船的吃水深度(船底与水面的距离)为4.25米,安全条例规定至少要有2米的安全间隙(船底与洋底的距离),该船在一天内(0:00~24:00)何时能进入港口然后离开港口?每次在港口能停留多久?
| 时刻 | 2:00 | 5:00 | 8:00 | 11:00 | 14:00 | 17:00 | 20:00 | 23:00 |
| 水深(米) | 7.5 | 5.0 | 2.5 | 5.0 | 7.5 | 5.0 | 2.5 | 5.0 |
(1)根据以上数据,求出函数f(t)=Asin(ωt+ϕ)+b的表达式;
(2)一条货船的吃水深度(船底与水面的距离)为4.25米,安全条例规定至少要有2米的安全间隙(船底与洋底的距离),该船在一天内(0:00~24:00)何时能进入港口然后离开港口?每次在港口能停留多久?
12.执行如图所示的程序框图,若输出的a的值为15,则判断框应填写( )
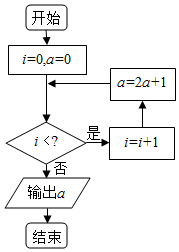

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
2.阅读程序框图,则该程序运行后输出的k的值是( )


| A. | 3 | B. | 4 | C. | 5 | D. | 6 |