题目内容
16.在平面直角坐标系xoy中,圆的参数方程为$\left\{\begin{array}{l}x=2+cosφ\\ y=2\sqrt{3}+sinφ\end{array}\right.$(φ为参数),以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,直线l的极坐标方程为$\sqrt{3}ρcosθ+3ρsinθ+4\sqrt{3}=0$.(1)将圆的参数方程化为普通方程,在化为极坐标方程;
(2)若点P在直线l上,当点P到圆的距离最小时,求点P的极坐标.
分析 (1)求出圆的标准方程,根据x=ρcosθ,y=ρsinθ,求出极坐标方程即可;
(2)求出直线l的直角坐标方程,联立方程组,求出P的坐标,从而求出P的极坐标即可.
解答 解:(1)将圆的参数方程,消去参数φ,
得:(x-2)2+${(y-2\sqrt{3})}^{2}$=1,
将x=ρcosθ,y=ρsinθ代入(x-2)2+${(y-2\sqrt{3})}^{2}$=1,
得圆的极坐标方程是:ρ2-4ρcosθ-4$\sqrt{3}$sinθ+15=0;
(2)由ρcosθ=x,ρsinθ=y知,
直线l的直角坐标方程为:$\sqrt{3}$x+3y+4$\sqrt{3}$=0,其斜率是-$\frac{\sqrt{3}}{3}$,
易得直线l与圆相离,
当点P到圆的距离最小时,则点P与圆心连线与直线l垂直,即其相离是$\sqrt{3}$,
其方程是:y-2$\sqrt{3}$=$\sqrt{3}$(x-2),即y=$\sqrt{3}$x,
联立方程组$\left\{\begin{array}{l}{\sqrt{3}x+3y+4\sqrt{3}=0}\\{y=\sqrt{3}x}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=-1}\\{y=-\sqrt{3}}\end{array}\right.$,
即点P的直角坐标是(-1,-$\sqrt{3}$),
故P的极坐标是(2,$\frac{4π}{3}$).
点评 本题考查了极坐标以及直角坐标方程的转化,考查转化思想,是一道中档题.

练习册系列答案
相关题目
4.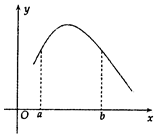 函数f(x)的图象如图所示,设f'(x)是f(x)的导函数,若0<a<b,下列各式成立的是( )
函数f(x)的图象如图所示,设f'(x)是f(x)的导函数,若0<a<b,下列各式成立的是( )
 函数f(x)的图象如图所示,设f'(x)是f(x)的导函数,若0<a<b,下列各式成立的是( )
函数f(x)的图象如图所示,设f'(x)是f(x)的导函数,若0<a<b,下列各式成立的是( )| A. | $f'({\frac{2ab}{a+b}})<f'({\frac{a+b}{2}})<f'({\sqrt{ab}})$ | B. | $f'({\frac{2ab}{a+b}})<f'({\sqrt{ab}})<f'({\frac{a+b}{2}})$ | ||
| C. | $f'({\frac{a+b}{2}})<f'({\frac{2ab}{a+b}})<f'({\sqrt{ab}})$ | D. | $f'({\frac{a+b}{2}})<f'({\sqrt{ab}})<f'({\frac{2ab}{a+b}})$ |
11.已知(x+$\frac{a}{x}$)n(n∈N,n>5)展开式的第5项是70,则展开式各项系数和是( )
| A. | 1 | B. | -1 | C. | 28或0 | D. | 29或0 |