题目内容
设Sn为等比数列{an}的前n项和，已知3S3=a4-2，3S2=a3-2，则公比q=（ ）
| A、3 | B、4 | C、5 | D、6 |
考点：等比数列的通项公式
专题：等差数列与等比数列
分析：根据3S3=a4-2，3S2=a3-2，结合当n≥2时有an=Sn-Sn-1，两式相减得a3与a4的关系，进而求出公比q．
解答：
解：由题意得，3S3=a4-2 ①，
3S2=a3-2 ②，
①-②得，3a3=a4-a3，
即a4=4a3，则q=
=4，
故选：B．
3S2=a3-2 ②，
①-②得，3a3=a4-a3，
即a4=4a3，则q=
| a4 |
| a3 |
故选：B．
点评：本题考查等比数列的通项公式与前n项和公式，以及当n≥2时有an=Sn-Sn-1，属于基础题．
练习册系列答案
相关题目
已知集合M={x|y=
，x∈Z}，N={y|y=3x+1，x∈R}，则M∩N的真子集个数为（ ）
| 4-x2 |
| A、5 | B、7 | C、31 | D、3 |
设a、b是两条直线，α、β是两个平面，a?α，b⊥β，则“a⊥b”是“α∥β”的（ ）
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充分必要条件 |
| D、既非充分也非必要条件 |
若f（x）=x2+bx+c，且f（1）=0，f（2）=0，则f（-1）=（ ）
| A、6 | B、-6 | C、5 | D、-5 |
设全集U=R，函数y=lg（2-x）的定义域为A，则∁∪A等于（ ）
| A、[2，+∞） |
| B、（-∞，2） |
| C、（0，2） |
| D、[0，2） |
中心点在原点，准线方程为x=±4，离心率为
的椭圆方程是（ ）
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、x2+
|
等差数列{an}中，a3=5，a5=9，则这个等差数列的公差为（ ）
| A、4 | B、3 | C、2 | D、1 |
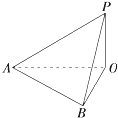如图，地面上有一旗杆OP，为了测得它的高度，在地面上选一基线AB，测得AB=20m，在A处测得点P的仰角为30°，在B处测得点P的仰角为45°，同时可测得∠AOB=60°，求旗杆的高度（结果保留1位小数）．