题目内容
已知正项等比数列{an}是递增数列,且满足a1+a5=246,a2a4=729.
(1)求数列{an}的通项公式;
(2)设bn=an•log3an+1(n∈N*),数列{bn}的前n项和为Tn,求Tn.
(1)求数列{an}的通项公式;
(2)设bn=an•log3an+1(n∈N*),数列{bn}的前n项和为Tn,求Tn.
考点:等差数列与等比数列的综合
专题:计算题,等差数列与等比数列
分析:(1)利用a1+a5=246,a2a4=729,建立方程组,求出首项与公比,即可求数列{an}的通项公式;
(2)确定数列{bn}的通项,利用错位相减法,即可求Tn.
(2)确定数列{bn}的通项,利用错位相减法,即可求Tn.
解答:
解:(1)∵
,∴
或
(舍去),
∴q=3,∴an=3n…(6分)
(2)由(1)得bn=(n+1)•3n,则Tn=2×3+3×32+…+n×3n-1+(n+1)×3n①3Tn=2×32+3×33+…+n×3n+(n+1)×3n+1②
①-②得-2Tn=6+(32+33+…+3n)-(n+1)•3n+1=3+
-(n+1)•3n+1=
-
•3n+1,
∴Tn=-
+
•3n+1
|
|
|
∴q=3,∴an=3n…(6分)
(2)由(1)得bn=(n+1)•3n,则Tn=2×3+3×32+…+n×3n-1+(n+1)×3n①3Tn=2×32+3×33+…+n×3n+(n+1)×3n+1②
①-②得-2Tn=6+(32+33+…+3n)-(n+1)•3n+1=3+
| 3(1-3n) |
| 1-3 |
| 3 |
| 2 |
| 2n+1 |
| 2 |
∴Tn=-
| 3 |
| 4 |
| 2n+1 |
| 4 |
点评:本题为等差等比数列的综合应用,用好错位相减法是解决问题的关键,属中档题.

练习册系列答案
相关题目
已知数列{an}的通项公式是an=n2sin(
π),则a1+a2+a3+…+a2014=( )
| 2n+1 |
| 2 |
A、
| ||
| B、2013×1007 | ||
| C、2014×1007 | ||
| D、2015×1007 |
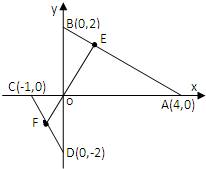 在直角坐标系中,已知A(4,0),B(0,2),C(0,-2),点E在线段AB(不含端点)上,点F在线段CD上,E、O、F三点共线.
在直角坐标系中,已知A(4,0),B(0,2),C(0,-2),点E在线段AB(不含端点)上,点F在线段CD上,E、O、F三点共线.