题目内容
8.已知f(x)=$\frac{{2}^{x}}{{2}^{x}+1}$+ax+cos2x,若f($\frac{π}{3}$)=2,则f(-$\frac{π}{3}$)等于( )| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
分析 得到f(-x)=$\frac{1}{{2}^{x}+1}$-ax+cos2x=1+2cos2x-f(x),由f($\frac{π}{3}$)=2,代入求出即可.
解答 解:∵f(x)=$\frac{{2}^{x}}{{2}^{x}+1}$+ax+cos2x=1-$\frac{1}{{2}^{x}+1}$+ax+cos2x,
∴f(-x)=$\frac{1}{{2}^{x}+1}$-ax+cos2x=1+2cos2x-f(x),
由f($\frac{π}{3}$)=2,
则f(-$\frac{π}{3}$)=1+2cos$\frac{2π}{3}$-f($\frac{π}{3}$)=-2,
故选:A.
点评 本题考查了函数求值问题,考查三角函数问题,是一道基础题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
18.函数f(x)=sin(2x+$\frac{π}{3}$)的图象向左平移φ(φ>0)个单位后关于原点对称,则φ的最小值为( )
| A. | $\frac{5π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
19.已知四个无穷数列{(-1)n$\frac{1}{n}$},{(-1)n$\frac{1}{{2}^{n}}$},{$\frac{{3}^{n-1}}{{2}^{n+2}}$},{$\frac{1{0}^{10}}{{n}^{2}}$},当n→∞时,这四个数列极限为0的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.已知a>0,a≠1,x≠0,则${log_{a^2}}{x^2}$=( )
| A. | 2logax | B. | logax | C. | 2loga|x| | D. | loga|x| |
11.设P={x|x<1},下列关系式成立的是( )
| A. | ∅∈P | B. | 0∉P | C. | 0⊆P | D. | {0}⊆P |
8.执行如图所示的程序框图,则输出的S的值是( )
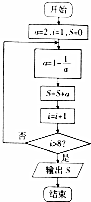

| A. | $\frac{9}{2}$ | B. | $\frac{5}{2}$ | C. | 3 | D. | $\frac{7}{2}$ |
9.若在区间[-1,2]中随机地取一个数x,则事件“0≤x≤2”发生的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |