题目内容
8．方程ex=2-x的根位于（ ）| A． | （-1，0） | B． | （0，1） | C． | （1，2） | D． | （2，3） |
分析 设函数f（x）=ex+x-2，根据根的存在性定理进行判断即可．
解答 解：设f（x）=ex+x-2，则f（0）=1-2=-1＜0，
f（1）=e+1-2=e-1＞0，
所以根据零点存在性定理，在区间（0，1）上函数f（x）存在一个零点，
即程ex=2-x的根位于（0，1）．
故选B．
点评 本题主要考查根的存在性定理的应用，利用根的存在性定理主要判断区间端点处的符号相反即可．
练习册系列答案
相关题目
18．在△ABC中，命题p：“B≠60°”，命题q：“△ABC不是等边三角形”，那么p是q的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分又不必要条件 |
19．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0），点A、F分别为其右顶点和右焦点，B1（0，b），B2（0，-b），若B1F⊥B2A，则该双曲线的离心率为（ ）
| A． | $1+\sqrt{5}$ | B． | $\frac{{\sqrt{5}-1}}{2}$ | C． | $\frac{{\sqrt{5}+1}}{2}$ | D． | $\sqrt{5}-1$ |
16．定义在R上的函数f（x）=2|x-m|-1为偶函数，记a=f（log0.53），b=f（log25），c=f（2m），则（ ）
| A． | a＜b＜c | B． | a＜c＜b | C． | c＜a＜b | D． | c＜b＜a |
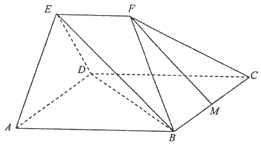已知：平行四边形ABCD中，∠DAB=45°，AB=$\sqrt{2}$AD=2$\sqrt{2}$，平面AED⊥平面ABCD，△AED为等边三角形，EF∥AB，EF=$\sqrt{2}$，M为线段BC的中点．
B．
C．
D．